一些2D几何算法

这里介绍了一些几何算法

有关面积的计算

三角形面积的计算

有很多的方法：

知道三条边长a,b,c的话可以使用海伦公式:

$$ p = \frac{1}{2}(a + b + c) \ S = \sqrt{p(p-a)(p-b)(p-c)} $$
知道三个顶点可以使用向量叉积:

$$ S = |\frac{1}{2}\vec{AB} \times \vec{AC}| = |\frac{1}{2}|\vec{AB}||\vec{AC}|\sin{\theta}| $$

四边形的面积计算

知道四条边长：

$$ p = \frac{1}{2}(a+b+c+d) \ S = \sqrt{p(p-a)(p-b)(p-c)(p-d)} $$
平行四边形，知道四个顶点坐标：

$$ S = \vec{AB} \times \vec{AC} $$

不规则多边形面积计算

其实也很简单，将多边形拆成多个三角形即可，使用$S=\frac{\vec{AB}\times \vec{AC}}{2}$：

假设顶点是顺时针排列的（记为$V[i]$）。我们可以在空间中任选一点$P$，然后顺时针遍历顶点并构造三角形，然后计算所有三角形面积再求和：

$$ S = \frac{1}{2}(\vec{PV_0} \times \vec{PV_1} + \vec{PV_1} \times \vec{PV_2} + \cdots \vec{PV_{n-1}} \times \vec{PV_n} + \vec{PV_n} \times \vec{PV_0}) $$

很容易可以看出这个公式在做什么：

假设点在多边形内，那么有：

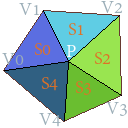
显然，$S_0 + S_1 + S_2 + S_3 + S_4$就是其面积（不需要加绝对值，因为顶点是顺时针排列，所以叉积的结果也是正的）

当点在多边形外，有：

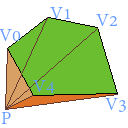
这个时候，$\vec{PV_3}\times \vec{PV_4}$和$\vec{PV_4}\times \vec{PV_5}$的面积都是负数，可以抵消到之前所有三角形面积和中多出的那一部分。

也可以通过此方法来判断多边形的顶点是否是按顺时针排列，如果最后面积大于0就是顺时针，否则是逆时针。

各种相交判断

判断点是否在线段上

使用点积或叉积判断是否在线段所在直线上，然后判断点是否在线段构成的矩形内，不然点可能在线段的延长线上：

1
2
3
4
5
6
7


bool PointInSegment(const Point& p, const Point& v1, const Point& v2) {
    return // 首先使用叉积判断点是否在线段所在直线上
           p.x * (v2.y - v1.y) - p.y * (v2.x - v1.x) == 0 &&
           // 然后判断是否在线段构成的矩形内
           min(v1.x, v2.x) <= p.x && p.x <= max(v1.x, v2.x) &&
           min(v1.y, v2.y) <= p.y && p.y <= max(v1.y, v2.y);
}

判断AABB矩形是否相交以及求出相交矩形

判断AABB矩形是否相交很简单：

1
2
3
4
5
6
7


bool IsRectIntersect(const Rect& r1, const Rect& r2) {
    float cx1 = std::max(r1.x, r2.x),
          cy1 = std::max(r1.x, r2.x),
          cx2 = std::min(r1.x + r1.w, r2.x + r2.w),
          cy2 = std::min(r1.y + r1.h, r2.y + r2.h);
    return (cx1 < cx2) || (cy1 < cy2);
}

(cx1, cy1)和(cx2, cy2)其实就是相交矩形的右下角顶点和左上角顶点。如果右下角顶点在左上角顶点左上方的话，那矩形就不相交了。

判断两线段是否相交

分为两步：

快速排斥实验：判断两线段构成的矩形是否相交，如果矩形不相交线段也一定不相交
跨立实验：使用叉积来判断两线段是否相交：

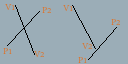
如果像左边一样相交，那么$\vec{V_1V_2}\times \vec{V_1P_1}$，$\vec{V_1V_2}\times \vec{V_1P_2}$一定是异号的，并且同理，$\vec{P_1P_2}\times \vec{P_1V_1}$和$\vec{P_1P_2}\times \vec{P_1V_2}$也是异号的。

如果不相交（如右边），则会有$\vec{P_1P_2}\times \vec{P_1V_2}$和$\vec{P_1P_2}\times \vec{P_1V_1}$同号。

1
2
3
4
5
6
7
8


bool SegmentIntersect(const Point& p1, const Point& p2,
                      const Point& v1, const Point& v2) {
    if (!IsRectIntersect(Rect(p1, p2), Rect(v1, v2))) return false;
    Point p_dir = p2 - p1,
          v_dir = v2 - v1;
    return Cross(p_dir, v1 - p1) * Cross(p_dir, v2 - p1) <= 0 &&
           Cross(v_dir, p1 - v1) * Cross(v_dir, p2 - v1) <= 0;
}

注意第一步快速排斥实验其实也可以不做，但是快速排斥实验很快，在两个线段离得远的时候可以快速返回false而不用进行第二步的叉乘。

判断线段和直线是否相交

和上面判断两线段是否相交差不多，也是使用跨立实验（假设线段两端点为$P_1\ P_2$）：

任取直线$L$上一点$Q$，和直线的方向向量$\vec{V}$，如果$\vec{QP_1}\times \vec{V}$和$\vec{QP_2}\times \vec{V}$异号，则相交。

判断AABB矩形和圆是否相交

有很多方法：

先判断矩形是否在圆内（四个顶点到圆心的距离小于圆半径），如果是则相交，否则看圆心到矩形四条边的距离，有小于圆半径的则相交
将矩形的四条边延长，将空间平分为九份：
- 如果圆心在矩形内则相交，否则
- 若圆心在矩形的上，下，左，右侧，则直接看圆心和对应边的距离，小于半径则相交
- 若圆心在矩形的左上，左下，右上，右下，则直接看圆心到对应顶点的距离，小于半径则相交

第一种方法代码简单，但是计算较多。第二种方法代码复杂，但是每条分支的计算很少。

判断点是否在多边形内

Crossing Number Method

此算法基于一个定理：从给定点发出一条射线，如果此点在多边形内，那么这条射线和多边形的交点一定是奇数个，否则是偶数个。

那么这里要解决的问题就是：

如何判断射线和边相交

判断射线和边相交很简单，我们先要做两个规定：

顶点按照顺时针排列
我们不要使用复杂的射线，直接用$x = x_0$这条穿过P点的竖直向上的射线。

首先要判断此边是否可能和直线相交：

$$ x_n\le x_0 \le x_{n+1} 或\ x_{n+1} \le x_0 \le x_n $$

然后我们要判断此边是否在直线上方：

$$ \frac{y_0 - y_n}{x_0 - x_n} \lt k $$

使用斜率进行判断即可。

当这两个条件都满足，此边即和直线相交，那么对相交点的计数就+1.

整个的代码可以是这样：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


bool Contains(const std::array<Point>& vertices, const Point& p) {
    for (size_t i = 0; i < vertices.size(); i++) {
        int crossing = 0;
        const Point& v1 = vertices[i],
                     v2 = vertices[(i + 1 % vertices.size())];
        double slope = (v2.y - v1.y) / (v2.x - v1.x);
        bool cond1 = v1.x <= p.x && p.x <= v2.x,
             cond2 = v2.x <= p.x && p.x <= v1.x,
             above = (p.y - v1.y) / (p.x - v1.x) < slope;

        if ((cond1 || cond2) && above) crossing ++;
    }
    return crossing % 2 == 0;
}

这里cond1和cond2分别对应于顶点顺时针排列和逆时针排列的情况。

这里要注意的是slope处可能出现除0错误，你可以在计算above变量的时候将除法去掉来避免：

1
2


// 不计算slope，直接在above上计算
bool above = (p.y - v1.y) * (v2.x - v1.x) < (p.x - v1.x) * (v2.y - v1.y)

Winding Number Method

这个算法利用叉乘的方向性，和上面多边形求面积方法差不多：如果$\vec{PV_0}\times \vec{PV_1}，\vec{PV_1}\times \vec{PV_2}，\cdots，\vec{PV_{n-1}}\times \vec{PV_n}和\vec{PV_n}\times \vec{PV_0}$ 所得结果的符号都一样的话，那么点就是在多边形内部，否则就是在外部。

判断射线和多边形相交

很简单，假设射线起点为$P$，射线方向为$\vec{D}$，多边形顶点为$V_i$，那么对所有的$\vec{PV_i}\times \vec{D}$的结果都同号的话就是不相交，出现异号就是相交。

判断射线和圆相交

假设射线起点为$P$，方向为$\vec{D}$，圆心为$Q$，半径为$R$。

分两步：

首先判断射线的方向是否朝向圆，若$\vec{PQ}\cdot \vec{D} \lt 0$即不朝向圆，那么一定不相交
否则，使用点到直线距离公式即可判断：$\frac{Ax+By+C}{\sqrt{A^2 + B^2}} \le R$则相交（或者用叉乘也行：$\frac{\vec{PQ}\times \vec{D}}{|\vec{D}|} \le R$即相交）

将凸多边形顶点按照顺时针排列

顺时针排列顶点问题在凹多边形下没有唯一解，所以这里只有凸多边形的情况，算法很简单：

找到最左边的点（x坐标最小）
将这个点和其他点连线，算出直线斜率，然后按照斜率进行排序即可

将简单多边形拆分成数个三角形

未完成

一些2D几何算法

相关文章：