本文讲述了MVP矩阵的意义,投影变换（透视投影和平行投影）矩阵的推导以及视口变换

模型变换

模型变换是将物体从原点移动到他应该在的位置（世界坐标）

视图变换

视图变换主要指摄像机变换。因为存在规定：

• 摄像机坐标必须在原点

• 摄像机看向$-z$轴

所以我们需要一些变换作用在世界中的所有物体上，以便于将他们变换到摄像机坐标。

投影变换

这是最后一步，将三维空间的物体（程序中记录的所有物体）投影到二维空间（屏幕）上从而显示他们。

平行投影

平行投影很简单：

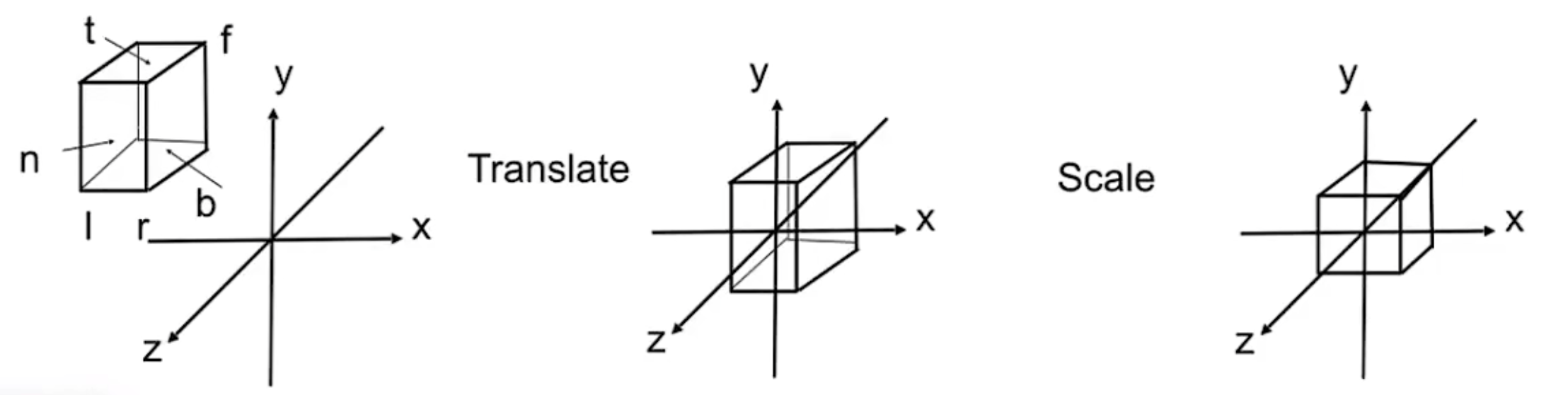
我们的可视范围在这个最左边的长方体里面，我们的目标是将其变换成最右边的标准立方体（即$x, y, z \in [-1, 1]$）。

很简单，先将长方体中心平移到原点（图中间的情况），然后再对长方体进行缩放即可：

$$ \begin{bmatrix} \frac{2}{right - left} & 0 & 0 & 0 \ 0 & \frac{2}{top - bottom} & 0 & 0 \ 0 & 0 & \frac{2}{near - far} & 0 \ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & -\frac{left + right}{2} \ 0 & 1 & 0 & -\frac{top + bottom}{2} \ 0 & 0 & 1 & -\frac{near + far}{2} \ 0 & 0 & 0 & 1 \end{bmatrix} = \ \begin{bmatrix} \frac{2}{right - left} & 0 & 0 & -\frac{left + right}{right - left} \ 0 & \frac{2}{top - bottom} & 0 & -\frac{top + bottom}{top - bottom} \ 0 & 0 & \frac{2}{near - far} & -\frac{near + far}{near - far} \ 0 & 0 & 0 & 1 \end{bmatrix} $$

正交投影

正交投影的推导比较麻烦:

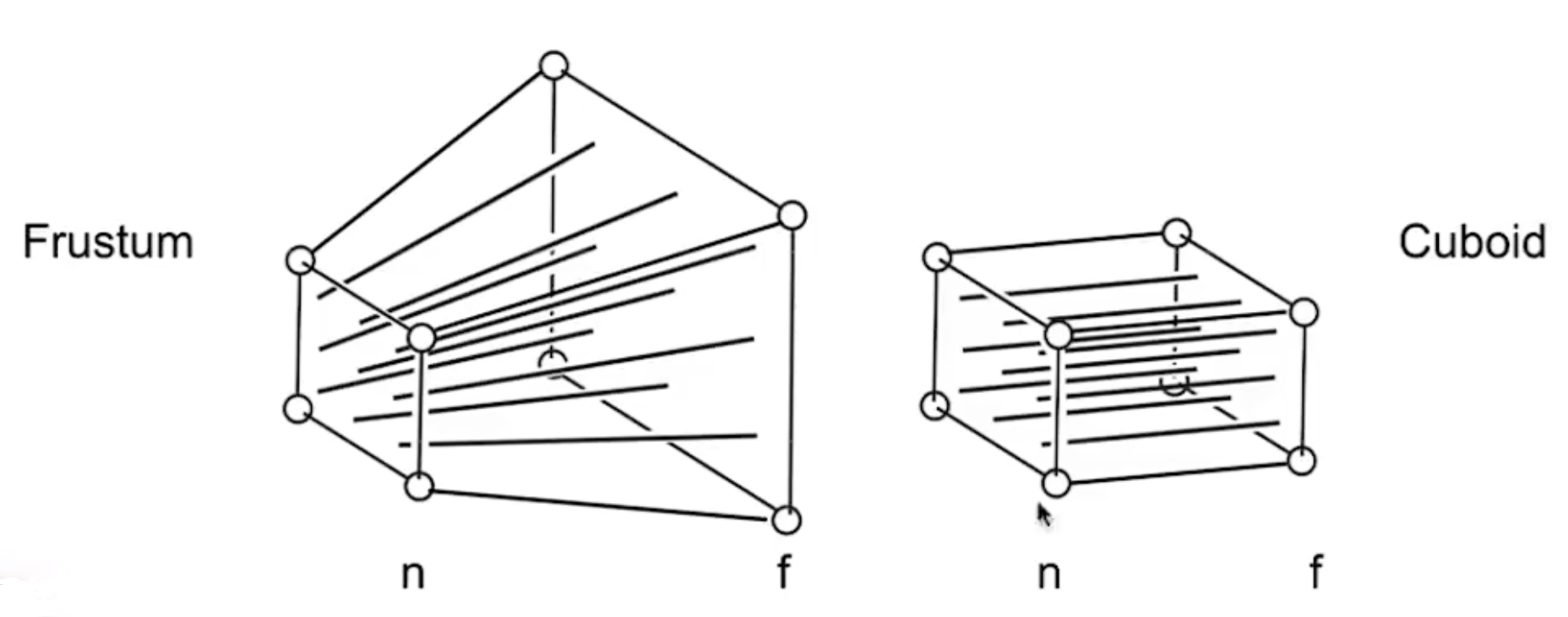
我们采用从平行投影推导到正交投影的方法，你可以想像将透视投影（Frustum）的远平面进行挤压，从而让其四条线平行来得到平行投影。

对于透视投影，我们有如下规定：

• 挤压前后近平面和远平面位置保持不变（即透视投影和平行投影的近，远平面的z值是一样的）

• 进平面上的点挤压前后不会发生变化

• 远平面的中心点挤压前后不会发生变化

有了上面两条规定，就可以推导出透视投影了，这里的公式为：

$$ M_{persp} = M_{ortho}M_{persp_to_ortho} $$

我们现在要求的就是$M_{persp_to_ortho}$矩阵。

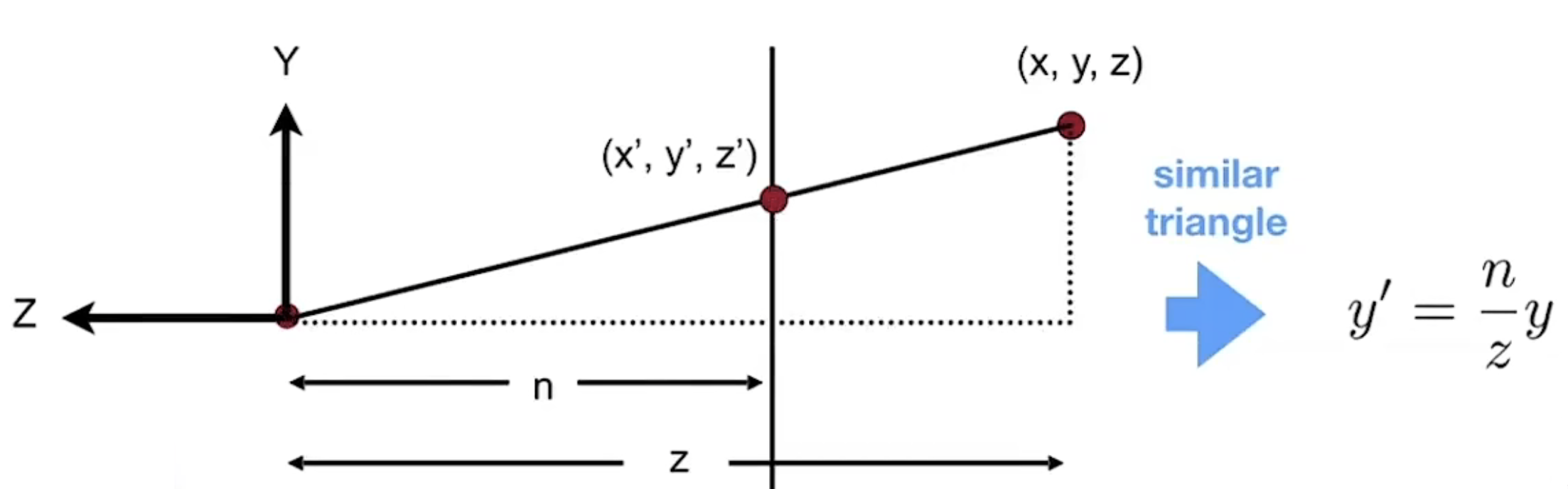
从侧面来看这个Frustum，$(x, y, z)$是视锥内的一点，$(x^{'},y^{'},z^{'})$是其经过变换后的点（确定这个点的方法是从原点做到$(x, y, z)$点的直线，和近平面的交点）

显然，由相似三角形得知：

$$ y^{'} = \frac{n}{z}y $$

那么同理，x的坐标也可以知道：

$$ x^{'} = \frac{n}{z}x $$

那么我们现在已经知道两个坐标了，接下来就是解$z$坐标：

$$ \begin{pmatrix} x \ y \ z \ 1 \end{pmatrix} \Rightarrow \begin{pmatrix} \frac{n}{z}y \ \frac{n}{z}x \ ? \ 1 \end{pmatrix} $$

首先根据齐次坐标性质，对齐次向量乘上常数不改变向量表示的点，那么我们直接乘上$z$，将除式消去：

$$ \begin{pmatrix} x \ y \ z \ 1 \end{pmatrix} \Rightarrow \begin{pmatrix} \frac{n}{z}y \ \frac{n}{z}x \ ? \ 1 \end{pmatrix} {multiply\ z} \Rightarrow \begin{pmatrix} ny \ nx \ ? \ z \end{pmatrix} $$

那么我们现在的$M_{persp_to_ortho}$就是：

$$ M_{persp_to_ortho} = \begin{bmatrix} n & 0 & 0 & 0 \ 0 & n & 0 & 0 \ a & b & c & d \ 0 & 0 & 1 & 0 \end{bmatrix} $$

其中$a, b, c, d$都是未知量。

然后我们使用上面说的两条规定：

规定二告诉我们，近平面上的点在挤压前后不会发生变化，这意味着当$z=n$时，有：

$$ \begin{pmatrix} x \ y \ n \ 1 \end{pmatrix} \Rightarrow \begin{pmatrix} nx \ ny \ n^2 \ n \end{pmatrix} $$

也就是说通过$M_{persp_to_ortho}$矩阵的变换，有：

$$ \begin{pmatrix} a & b & c & d \end{pmatrix} \begin{pmatrix} x \ y \ n \ 1 \end{pmatrix} = n^2 $$

显然，最后的结果$n^2$和$x,y$没有半毛钱关系，这意味着一定有

$$ a = 0, b = 0 $$

那么我们可以得到方程：

$$ \begin{pmatrix} 0 & 0 & c & d \end{pmatrix} \begin{pmatrix} x \ y \ n \ 1 \end{pmatrix}

cn + d

n^2 $$

规定三告诉我们，远平面的中心点挤压之后也不发生改变，这意味着有：

$$ \begin{pmatrix} 0 & 0 & c & d \end{pmatrix} \begin{pmatrix} 0 \ 0 \ f \ 1 \end{pmatrix}

cf + d = f^2 $$

由上述两个方程联立可解得：

$$ \begin{matrix} c & = n + f \ d & = -nf \end{matrix} $$

这样结果就出来了：

$$ M_{persp_to_ortho} = \begin{bmatrix} near & 0 & 0 & 0 \ 0 & near & 0 & 0 \ 0 & 0 & near+far & -near far \ 0 & 0 & 1 & 0 \end{bmatrix} $$

$$ M_{persp} = M_{ortho}M_{persp_to_ortho} = \ \begin{bmatrix} \frac{2}{right - left} & 0 & 0 & -\frac{left + right}{right - left} \ 0 & \frac{2}{top - bottom} & 0 & -\frac{top + bottom}{top - bottom} \ 0 & 0 & \frac{2}{near - far} & -\frac{near + far}{near - far} \ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} near & 0 & 0 & 0 \ 0 & near & 0 & 0 \ 0 & 0 & near+far & -near\ far \ 0 & 0 & 1 & 0 \end{bmatrix}

\begin{bmatrix} \frac{2n}{r - l} & 0 & -\frac{r+l}{r-l} & 0 \ 0 & \frac{2n}{t-b} & -\frac{t+b}{t-b} & 0 \ 0 & 0 & \frac{n+f}{n-f} & \frac{2fn}{f-n} \ 0 & 0 & 1 & 0 \end{bmatrix} $$

OpenGL的做法则是对$n$和$f$取绝对值：

$$ \begin{bmatrix} \frac{2|n|}{r - l} & 0 & -\frac{r+l}{r-l} & 0 \ 0 & \frac{2|n|}{t-b} & -\frac{t+b}{t-b} & 0 \ 0 & 0 & \frac{|n|+|f|}{|n|-|f|} & \frac{2|f||n|}{|n|-|f|} \ 0 & 0 & -1 & 0 \end{bmatrix} \ $$

更一般的做法是通过四个参数来确定投影矩阵：

• fov：纵向的视角大小
• aspect：近平面的宽高比
• zNear：近平面到摄像机距离（即到原点距离）
• zFar：远平面到摄像机距离（即到原点距离）

通过这些可以计算出：

• 近平面高度H：$H = 2zNear\times \tan{\frac{fov}{2}}$
• 近平面宽度W：$W=2aspect\times zNear\times \tan{\frac{fov}{2}}$

这样可以得到

• $t = \frac{H}{2}$
• $b = -\frac{H}{2}$
• $l = -\frac{W}{2}$
• $r = \frac{W}{2}$

注意zNear和zFar是到原点的距离，不是近，远平面的坐标，所以为了和上面平行投影矩阵合二为一，我们需要用到的是近远平面坐标。假设进平面坐标为$n$，远平面坐标为$f$，就有：

$$ \begin{aligned} H &= 2|n|\times \tan{\frac{fov}{2}} \ W &= 2aspect\times |n|\times \tan{\frac{fov}{2}} \end{aligned} $$

最终的结果就是：

$$ \begin{bmatrix} \frac{2n}{W} & 0 & 0 & 0 \ 0 & \frac{2n}{H} & 0 & 0 \ 0 & 0 & \frac{n + f}{n - f} & \frac{2fn}{f - n} \ 0 & 0 & 1 & 0 \ \end{bmatrix} = \ \begin{bmatrix} \frac{n}{|n|aspect\times \tan{0.5fov}} & 0 & 0 & 0 \ 0 & \frac{n}{|n|\tan{0.5fov}} & 0 & 0 \ 0 & 0 & \frac{n + f}{n - f} & \frac{2fn}{f - n} \ 0 & 0 & 1 & 0 \ \end{bmatrix} $$

Viewport

w前面我们使用了投影矩阵将场景归一化到$[-1, 1]^3$中，而视口变换则是将$[-1,1]^3$转换到$[x, x+width]\times [y, y+height]\times [0, d]$上，也就是我们真正的屏幕坐标中。

$$ \begin{bmatrix} \frac{width}{2} & 0 & 0 & 0 \ 0 & \frac{height}{2} & 0 & 0 \ 0 & 0 & \frac{d}{2} & 0 \ 0 & 0 & 0 & 1 \end{bmatrix}

\begin{bmatrix} 1 & 0 & 0 & \frac{width}{2} + x \ 0 & 1 & 0 & \frac{height}{2} + y \ 0 & 0 & 1 & 1 \ 0 & 0 & 0 & 1 \end{bmatrix}

=

\begin{bmatrix} \frac{width}{2} & 0 & 0 & \frac{width}{2} + x \ 0 & \frac{height}{2} & 0 & \frac{height}{2} + y \ 0 & 0 & \frac{d}{2} & 1 \ 0 & 0 & 0 & 1 \end{bmatrix} $$

一般的屏幕坐标是以窗口左上角为原点，x轴向右，y轴向下。现在我们视口的中心是在(0, 0)处也就是左上角原点位置，并且z值一般在(0, 1)之间。所以我们一般取$x = y = 0$，$d = 1$。