本文说了有关光栅化的事情
光栅化是什么
光栅化的基础单位是最简单的多边形:三角形。
光栅化做的事就是如下:
遍历屏幕中所有的点,判断点是否在三角形内
如果在三角形内,通过重心坐标计算出此点的z坐标,并且对其他顶点属性进行插值
将点传给片段着色器进行着色
其主要功能就是对三角形进行采样,确定其中的点传给片段着色器。
判断点是否在三角形内
首先要做的第一步就是判断点是否在三角形内。
我们光栅化的做法是这样:假设三角形坐标为,对屏幕上的每个点,判断其是否在三角形对XoY平面投影的区域内。
假设三角形的三个顶点是$(x_1, y_1, z_1)$,$(x_2, y_2, z_2)$,$(x_3, y_3, z_3)$,那么他对XoY的投影点是$(x_1, y_1)$,$(x_2, y_2)$,$(x_3, y_3)$,我们就要对屏幕上每个点判断其是否在这三个顶点所围成的三角形内部。
Edge Equation
Edge Equation算法使用叉积来判断:
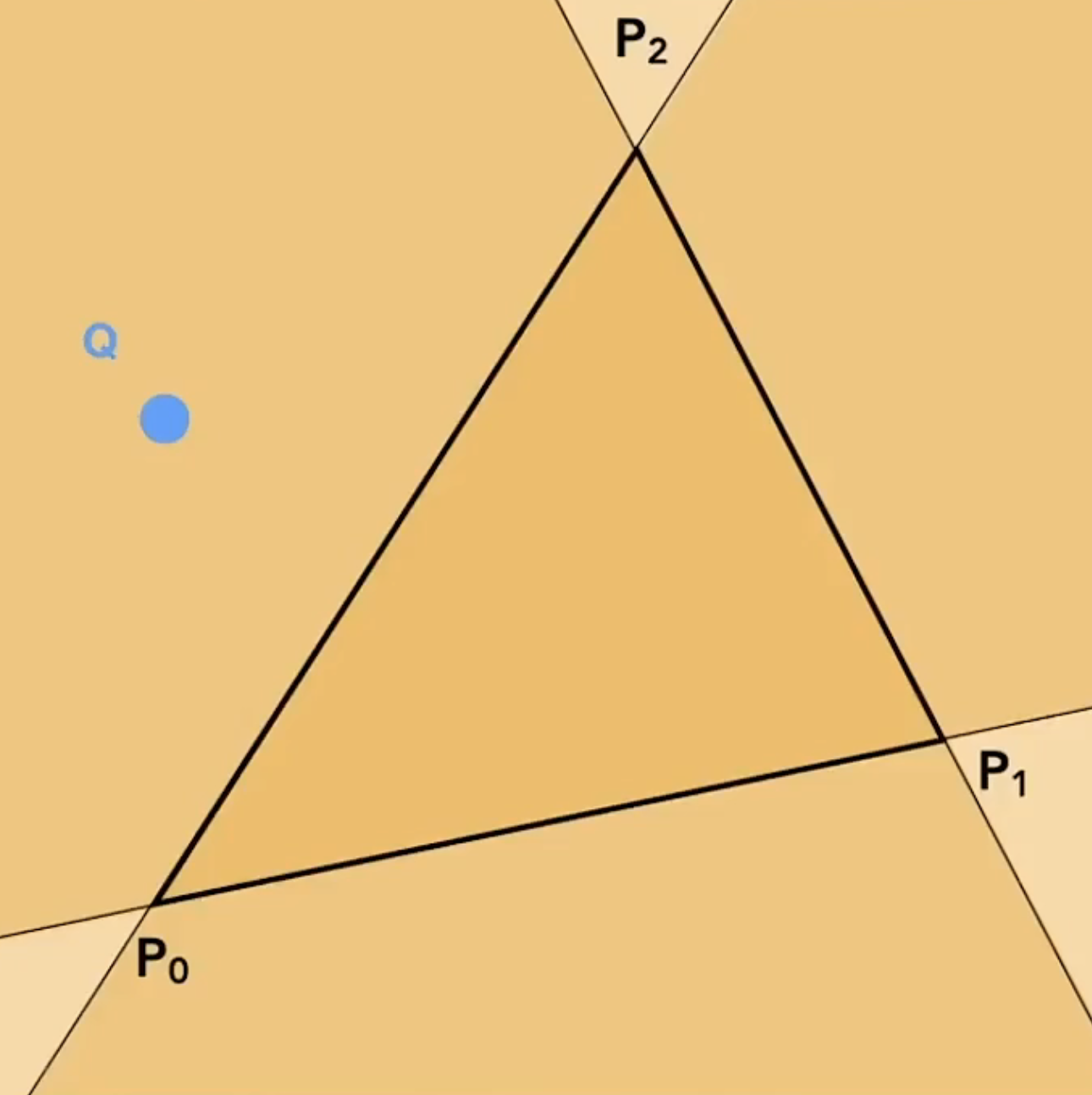
当Q点在三角形外面时,$\vec{P_0P_1}\times \vec{P_0Q}$,$\vec{P_1P_2}\times \vec{P_1Q}$,$\vec{P_2P_0}\times \vec{P_2Q}$这三者的值一定有至少一个和其他两个的值的符号不一样。而当Q在内部时,符号一定是一样的。
注意这里向量的顺序一定是按照顺时针或逆时针,不要搞什么$\vec{P_0P_2},\vec{P_0P_1}$。
使用重心坐标
重心坐标主要是用来插值出点的z坐标,但是这里也可以使用它来判断三角形在不在内部。
首先看一下重心坐标的定义:
如果一个点$P$在三角形$V_1, V_2, V_3$内部,那么有:
$$ \begin{aligned} \vec{P} = \alpha \vec{V_1} + \beta \vec{V_2} + \gamma \vec{V_3} \ \alpha + \beta + \gamma = 1 \end{aligned} $$
这里第二个式子告诉我们,其实可以只使用$\alpha$和$\beta$来表示点P:
$$ \vec{P} = (1-\beta - \gamma) \vec{V_1} + \beta \vec{V_2} + \gamma \vec{V_3} $$
当$\alpha \beta \gamma$中任意一者为0时点在三角形边上,任意两个为0时点在三角形顶点上。任意一个为负数则表示点在三角形外面。我们可以使用这个来判断点在不在三角形中间。
那么接下来就是求解这三个未知数,有两种方法:
使用面积比来计算
第一种是通过重心坐标的性质:
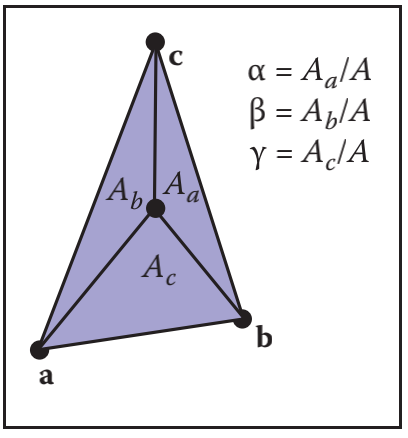
$\alpha,\beta,\gamma$的值为对应小三角形面积和整个三角形面积的比,所以我们就能使用向量叉乘的性质来算出这三个量:
$$ \begin{matrix} A = \frac{\vec{ca} \times \vec{ba}}{2} \ A_a = \frac{\vec{pc} \times \vec{pb}}{2} \ A_b = \frac{\vec{pa} \times \vec{pc}}{2} \ A_c = \frac{\vec{pa} \times \vec{pb}}{2} \ \end{matrix} $$
这样$\alpha,\beta,\gamma$就出来了。注意这里可能产生的除0错误:A的值为0。这意味着三角形退化成线或者点了,我们直接抛弃三角形。
推导出公式来计算
第二种是我们自己推导:
$$ \begin{matrix} & \vec{P} = (1-\beta - \gamma) \vec{V_1} + \beta \vec{V_2} + \gamma \vec{V_3} \ & \Downarrow \ & \vec{P} = \vec{V_1}-\beta \vec{V_1} - \gamma \vec{V_1} + \beta \vec{V_2} + \gamma \vec{V_3} \ & \Downarrow \ & \vec{P} - \vec{V_1} = \beta(\vec{V_2} - \vec{V_1}) + \gamma(\vec{V_3} - \vec{V_1}) \ & \Downarrow \ &\vec{PV_1} = \beta \vec{V_2V_1} + \gamma \vec{V_3V_1} \end{matrix} $$
把左边的$\vec{PV_1}$挪到右边,就有:
$$ \beta \vec{V_2V_1} + \gamma \vec{V_3V_1} + \vec{V_1P} = 0 $$
因为这里的所有向量都是二维向量,所以我们有:
$$ \begin{cases} \beta \vec{V_2V_1}_x + \gamma \vec{V_3V_1}_x + \vec{V_1P}_x = 0 \ \beta \vec{V_2V_1}_y + \gamma \vec{V_3V_1}_y + \vec{V_1P}_y = 0 \ \end{cases} $$
任意的线性方程组都可以写成矩阵形式,那么我们有:
$$ \begin{cases}
\begin{bmatrix} \beta & \gamma & 1 \end{bmatrix} \begin{bmatrix} \vec{V_2V_1}_x \ \vec{V_3V_1}_x \ \vec{V_1P}_x \end{bmatrix}
= 0 \
\begin{bmatrix} \beta & \gamma & 1 \end{bmatrix}
\begin{bmatrix} \vec{V_2V_1}_y \ \vec{V_3V_1}_y \ \vec{V_1P}_y \end{bmatrix}
= 0
\end{cases} $$
那么这就意味着$\begin{bmatrix} \beta & \gamma & 1 \end{bmatrix}$和另外两个向量的点乘为0,这意味着其和另外两个向量垂直。
那就好做了,直接对上面方程组右边两个向量做叉积:
$$ \begin{bmatrix} \vec{V_2V_1}_x \ \vec{V_2V_3}_x \ \vec{V_1P}_x \end{bmatrix}
\times
\begin{bmatrix} \vec{V_2V_1}_y \ \vec{V_2V_3}_y \ \vec{V_1P}_y \end{bmatrix}
=
\begin{bmatrix} a & b & c \end{bmatrix}
=
c \begin{bmatrix} \beta & \gamma & 1 \end{bmatrix} $$
这里我们算出来的向量是$\begin{bmatrix}\beta & \gamma & 1 \end{bmatrix}$的c倍,所以我们得对其除以c。
这个时候必须考虑$c = 0$的情况。由向量叉乘公式,c的计算过程其实是这样:
$$ c = \left| \begin{matrix} \vec{V_2V_1}_x & \vec{V_2V_3}_x \ \vec{V_2V_1}_y & \vec{V_2V_3}_y \ \end{matrix} \right|
\left| \begin{matrix} \vec{V_2V_1}_x & \vec{V_2V_1}_y \ \vec{V_2V_3}_x & \vec{V_2V_3}_y \ \end{matrix} \right| $$
上述行列式为0说明$\vec{V_2V_1}\times \vec{V_2V_3} = 0$,这意味着这两个向量共线,即三角形退化成直线了。
这里你可以抛弃三角形,或者绘制这条直线。
显然,方法二比起方法一更好,他只需要做一次叉乘就能得到结果。
使用三角形AABB包围盒加速判断
这里我们可以加速这一步骤:我们找到三角形的AABB包围盒,然后遍历屏幕上的点时先判断在不在包围盒内,不在就直接丢弃:
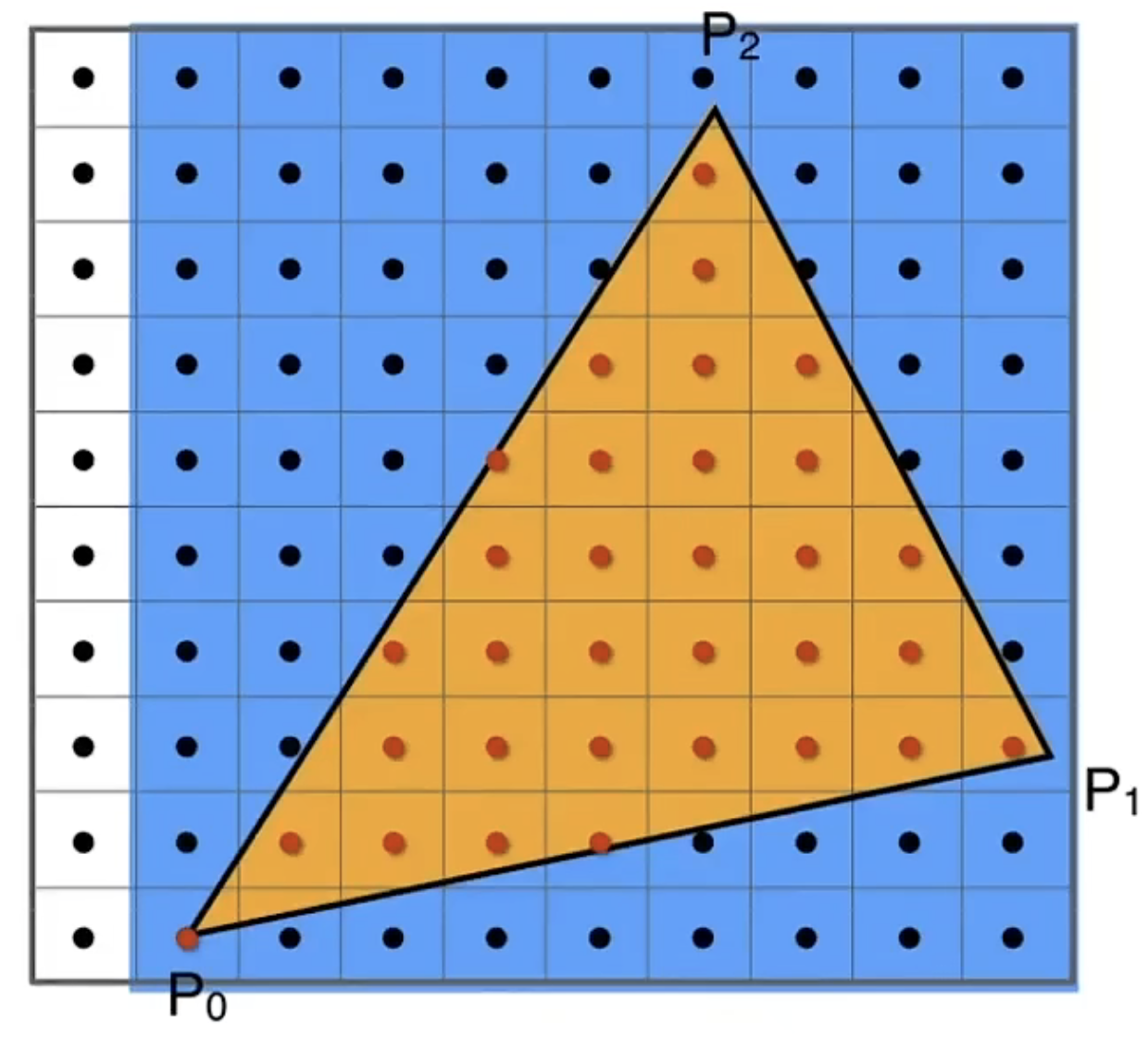
对三角形内的每个点求出z坐标
我们确定了三角形内的所有点,现在需要对每个点计算其z坐标。
平面方程法(推荐仅在平行投影中使用)
可以使用平面方程来解:
三角形所在平面的方程为:
$$ A(x-x_1)+B(y-y_1)+C(z-z_1) = 0 $$
而$(A, B, C)$又是此平面的法向量:
$$ \vec{V_1V_2} \times \vec{V_1V_3} = \begin{bmatrix} A & B & C \end{bmatrix} $$
那么就可以很容易求得此三角形所在平面的方程。然后对屏幕上的点$P(x, y)$,我们可以将其带入方程求得z坐标:
$$ z = \frac{x_1+y_1+z_1-Ax-By}{C} $$
当$C = 0$时意味着平面的法向量位于$XoY$平面内,这意味着从我们的视角看去,三角形变成了一条线。这个时候可以抛弃三角形。
z坐标的透视校正(透视投影中使用)
平面方程法只能在平行投影中使用,因为正交投影会让三角形“变形”,导致其z坐标和其他点并不是线性关系。所以我们需要对z坐标进行透视校正。
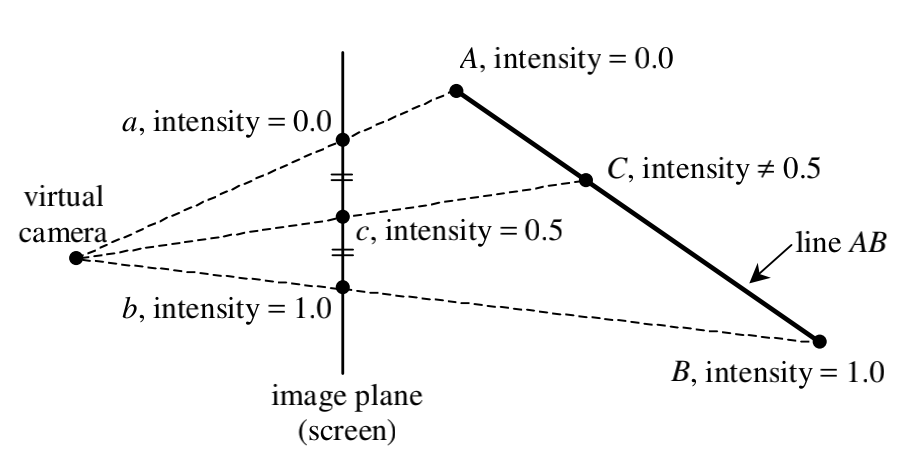
上图解释了为何需要透视校正。在屏幕上,c点位于a,b的中间,但在透视投影的情况下真正的点C并不位于AB之间,如果这时候还用线性关系去运算就会带来错误的结果。
接下来我们来算透视校正:
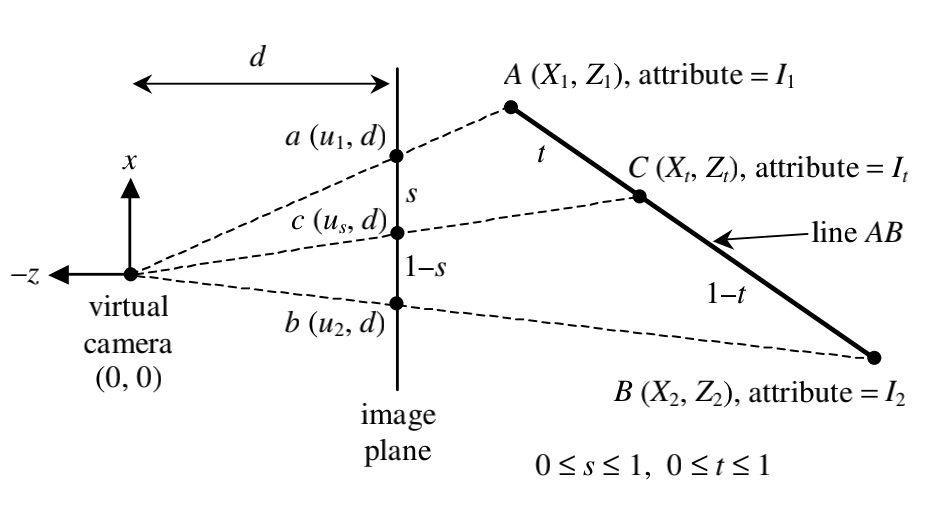
我们先从侧面看整个场景,研究二维的情况,然后将其推广到三维情况。
这里我们的摄像机看向z的正方向,近平面到摄像机的z距离为d。$s = \frac{|ab|}{|ac|}$,$t = \frac{|AC|}{|AB|}$。
首先,通过相似三角形可得:
$$ \frac{X_1}{Z_1} = \frac{u_1}{d} \Rightarrow X_1 = \frac{u_1}{d}Z_1 \tag{1} $$
$$ \frac{X_2}{Z_2} = \frac{u_2}{d} \Rightarrow X_2 = \frac{u_2}{d}Z_2 \tag{2} $$
$$ \frac{X_t}{Z_t} = \frac{u_s}{d} \Rightarrow X_t = \frac{u_s}{d}Z_t \tag{3} $$
然后由s的计算公式可以得到:
$$ s = \frac{u_2 - u_1}{u_s - u_1} \Rightarrow u_s = u_1 + (u_2 - u_1)s \tag{4} $$
同理,通过t的计算公式可以得到:
$$ X_t = X_1 + (X_2 - X_1)t \tag{5} $$
$$ Z_t = Z_1 + (Z_2 - Z_1)t \tag{6} $$
将$(4)$和$(5)$式代入$(3)$式可得:
$$ Z_t = \frac{d(X_1 + t(X_2 - X_1))}{u_1 + (u_2 - u_1)s} \tag{7} $$
再将$(1),(2)$代入$(7)$可得:
$$ Z_t = \frac{d(\frac{u_1Z_1}{d}+t(\frac{u_2Z_2}{d} - \frac{u_1Z_1}{d}))}{u_1 + s(u_2 - u_1)} \tag{8} $$
将$(6)$代入$(7)$:
$$ Z_1 + (Z_2 - Z_1)t = \frac{d(\frac{u_1Z_1}{d}+t(\frac{u_2Z_2}{d} - \frac{u_1Z_1}{d}))}{u_1 + s(u_2 - u_1)} \tag{9} $$
化简得
$$ t = \frac{sZ_1}{sZ_1 + (1-s)Z_2} \tag{10} $$
然后将$(10)$代入$(6)$:
$$ Z_t = Z_1 + \frac{sZ_1}{sZ_1 + (1-s)Z_2}(Z_2 - Z_1) $$
化简得:
$$ Z_t = \frac{1}{\frac{1}{Z_1}+s(\frac{1}{Z_2} - \frac{1}{Z_1})} $$
然后对$Z_t$取倒数:
$$ \frac{1}{Z_t} = \frac{1}{Z_1} + s(\frac{1}{Z_2} - \frac{1}{Z_1}) $$
这说明z的倒数之间是成正比的,也就是说,记$W = \frac{1}{Z}$,有:
$$ W_t = W_1 + s(W_2 - W_1) = (1-s)W_1 + sW_2 $$
这就是二维空间中的透视校正。
推广到三维空间中,我们就需要找到和$s$相对应的量。注意这里$s$是点c到点a的距离比,并且$s \in [0, 1]$。我们很容易想到一个和此有类似性质的东西:重心坐标。
所以推广到3D的公式就是这样:
$$ \frac{1}{Z_t} = \frac{\alpha}{Z_1} + \frac{\beta}{Z_2} + \frac{\gamma}{Z_3} $$
其中$\alpha, \beta, \gamma$三角形投影到近平面上的重心坐标参数。
重心坐标在透视投影的情况下会发生改变,那么其他的属性值也会发生改变。对于任意的属性值,我们可以用如下公式进行透视校正:
$$ \frac{1}{Z_t}I_t = \frac{\alpha}{Z_1}I_1 + \frac{\beta}{Z_2}I_2 + \frac{\gamma}{Z_3}I_3 $$
编程小技巧
这里因为$\frac{1}{Z}$之间成正比,所以我们一般会令$w = \frac{1}{Z}$。而通过上一章的透视投影矩阵推导,我们可以知道经过透视投影变换后得到的点为:
$$ \begin{bmatrix} x \ y \ z \ 1 \end{bmatrix}
\Rightarrow
\begin{bmatrix} zx \ zy \ z^2 \ z \end{bmatrix} $$
所以我们可以提前保留下$\frac{1}{Z}$,不仅是为了进行线性插值,在后面做透视除法(即给透视之后的点除以$z$)也可以直接乘上$\frac{1}{Z}$。