文本是Games101 Material and Appearance的笔记
BRDF材质
漫反射材质(Diffuse/Labertian Material)
我们知道BRDF其实就是对光线从表面反射出去的描述,所以BRDF就对应着漫反射材质。
这里我们假设,所有的入射光都是一样的,并且物体自己不发光,不吸收光(即反射出去的光和入射光一样),那么渲染方程就可以写成:
$$ L_o(\omega_o) = \int_{\Omega^+}f_r L_i(\omega_i)\cos{\theta}\text{d}\omega_i = f_rL_i\int_{\Omega^+}\cos{\theta}\text{d}\omega_i $$
最后的积分是对上半球的曲面积分,根据$\omega_i = \sin{\theta_i}\text{d}\theta\text{d}\phi$可以积分得到:
$$ L_o = f_rL_i\pi $$
那么有
$$ f_r = \frac{L_o}{L_i \pi} $$
将$L_o/L_i$记作$\rho$,可以得到BRDF:
$$ f_r = \frac{\rho}{\pi} $$
这里的$\rho$就是反射率($\rho \in [0, 1]$)。在实际应用中可以是表面的颜色。
Glossy材质(Glossy Material)
Glossy材质是一种类似于金属表面的材质,但是表面没有金属那么粗糙:

反射和折射材质(Ideal reflective/refractive material)
就和实际的透明材质一样,光线有一部分反射,另一部分折射。
反射的方向我们可以通过入射方向和法线计算得到:
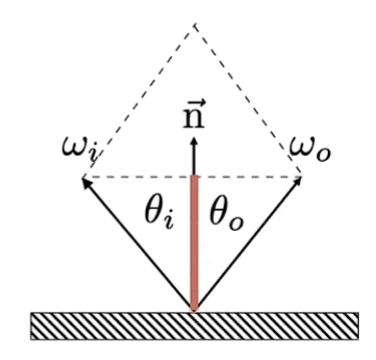
这里由反射的定义知,$\theta_i = \theta_o$,入射光线的反方向是$\omega_i$,我们要求出射光线$\omega_o$。
这里假设法向量是单位向量,那么我们有$\vec{\omega_i} + \vec{\omega_o} = 2\vec{n}Proj_{\vec{n}}\vec{\omega_o}$
然后使用点乘表示投影得到公式$2\vec{n}\frac{(\vec{\omega_o}\cdot\vec{n})}{|\vec{n}|} = \vec{\omega_i} + \vec{\omega_o}$
所以我们就可以求得:
$$ \vec{\omega_o} = 2\vec{n}(\vec{\omega_i}\cdot \vec{n}) - \vec{\omega_i} $$
折射则相对复杂一点。要计算折射的向量,就必须用到菲涅尔定理:
$$ \frac{n_1}{n_2} = \frac{\sin{\theta_1}}{\sin{\theta_2}} $$
这里$n_i$是介质的折射率,$\theta_i$是光线和平面发现的夹角。
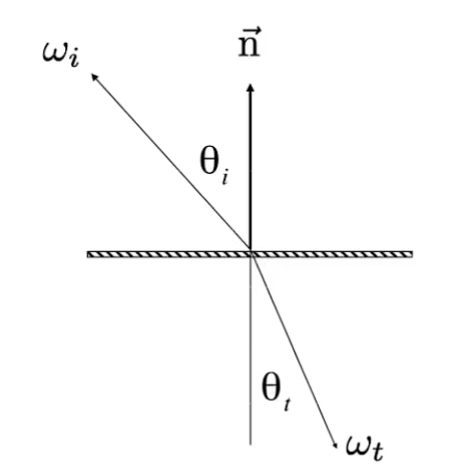
通过很简单的计算就能得出折射光线和法线的夹角了。