本文解释了TBN矩阵的推导和在顶点着色器中对切线空间变换的推导。

TBN矩阵推导

TBN即切线，副切线，法线的缩写(Tangent, Bitangent, Normal)，是用在法线贴图中用于将贴图中的法线转换到正确坐标的矩阵。

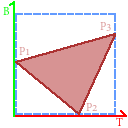
蓝色方框表示法线贴图的大小，红色三角形是我们要将发现贴图贴上去的三角形。我们的目标是求出T向量和B向量，然后使用叉乘可以得到N向量。这样TBN矩阵就完成了。 假设$P_i = (x_i,y_i,z_i)$，在$P_i$点的UV坐标为$(U_i, V_i)$, 那么有：

$$ \begin{align} \vec{P_2P_1} &= (U_1 - U_2)\vec{T} + (V_1 - V_2)\vec{B} \ \vec{P_2P_3} &= (U_3 - U_2)\vec{T} + (V_3 - V_2)\vec{B} \ \end{align} $$

这里设$\vec{T} = (T_x, T_y, T_z)，\vec{B} = (B_x, B_y, B_z)$，那么有方程组：

$$ \begin{align} \vec{P_2P_1} &= (U_1 - U_2)(T_x, T_y, T_z) + (V_1 - V_2)(B_x, B_y, B_z) \ \vec{P_2P_3} &= (U_3 - U_2)(T_x, T_y, T_z) + (V_3 - V_2)(B_x, B_y, B_z) \ \end{align} $$

显然，这可以写成矩阵形式：

$$ \begin{bmatrix} \vec{P_2P_1}_x & \vec{P_2P_1}_y & \vec{P_2P_1}_z \ \vec{P_2P_3}_x & \vec{P_2P_3}_y & \vec{P_2P_3}_z \ \end{bmatrix}

\begin{bmatrix} U_1 - U_2 & V_1 - V_2 \ U_3 - U_2 & V_3 - V_2 \ \end{bmatrix} \begin{bmatrix} T_x & T_y & T_z \ B_x & B_y & B_z \ \end{bmatrix} $$

这个方程很好解，直接左右同乘右边第一个方程的逆即可：

$$ \begin{bmatrix} T_x & T_y & T_z \ B_x & B_y & B_z \ \end{bmatrix}

\begin{bmatrix} U_1 - U_2 & V_1 - V_2 \ U_3 - U_2 & V_3 - V_2 \ \end{bmatrix}^{-1} \begin{bmatrix} \vec{P_2P_1}_x & \vec{P_2P_1}_y & \vec{P_2P_1}_z \ \vec{P_2P_3}_x & \vec{P_2P_3}_y & \vec{P_2P_3}_z \ \end{bmatrix} $$

这样T和B就解出来了，叉乘之后N也就解出来了。

顶点着色器中对TBN的变换

最简单使用TBN矩阵的方法是先在顶点着色器中随着模型矩阵一起变换，然后传入片段着色器。但是我们知道片段着色器的开销很大，所以这里有个方法是反过来做：使用TBN矩阵的逆矩阵乘上光源位置，片段位置和观察位置，将他们变换到切线空间中，这一步可以直接在顶点着色器中进行计算，从而节省片段着色器的开销：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

// 组装TBN矩阵
vec3 T = normalize(vec3(model * vec4(tangent, 0.0)));
vec3 B = normalize(vec3(model * vec4(bitangent, 0.0)));
vec3 N = cross(T, B);
mat3 TBN = mat3(T, B, N);

// 得到矩阵的逆（正交矩阵的逆为其转置）
TBN = transpose(TBN);

// 将光照信息转换到切线空间：
lightDir = TBN * lightDir;
viewDir = TBN * viewDir;
// ...