基于约束的物理求解

本文述说了基于约束的物理求解器，这是很多游戏物理引擎的核心。

理解约束

**约束(constraints)**是游戏物理引擎中的核心概念。

当物体在做曲线运动时，设定曲线的方程为$C(x, y)$，当物体在曲线上时满足$C(x,y)=0$

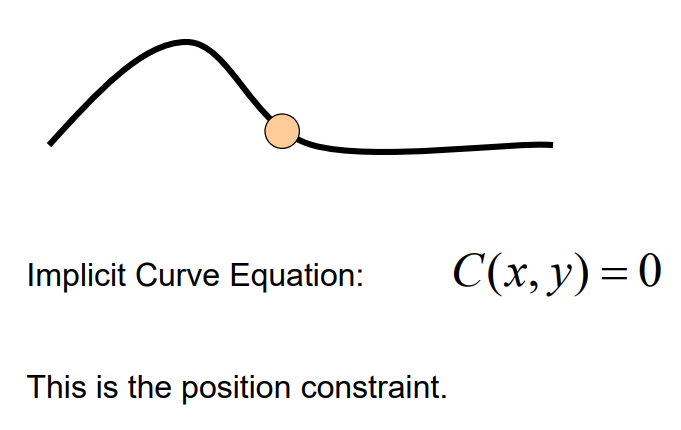
曲线运动的约束

这叫做位置约束，物体在运动时要满足这个约束方程才行。

物理引擎中的约束求解器不能求解位置约束，但可以求解速度约束。求$C(x,y)$的全导数可以得到速度： $$ \dot{C}(x,y) = 0 $$

求解纯圆周运动的约束

那么接下来通过一个具体场景来计算约束：物体被连杆连接在固定点，物体做圆周运动：

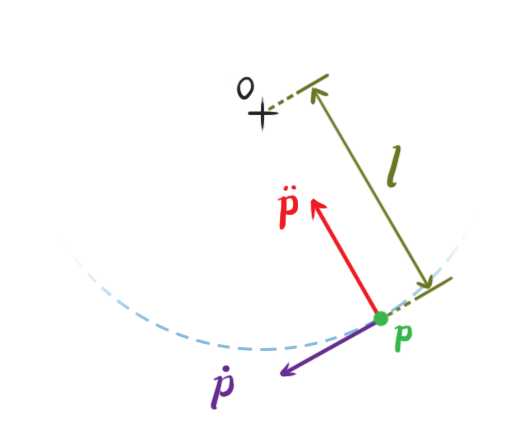
圆周运动中的物体约束

很显然，这里的位置约束为：物体$P_1$到固定点$P_2$的距离总是连杆的长度$l$，那么有： $$ C(x, y):\lVert P_1 - P_2 \rVert-l = 0 $$ 这里$P_1 - P_2$在物理中是物体相对于固定点$P_2$的相对位置我们记为$P_{21}$。那么约束变为： $$ C(P_{21}):\lVert P_{21} \rVert -l =0 $$ 我们的约束求解器只能对速度求解，所以对$C(P_{21})$对时间求导得到速度： $$ \dot{C}(P_{21}):(\dot{\lVert P_{21} \rVert - l}) =\dot{\lVert P_{21} \rVert}=\dot{\sqrt{P_{21} \cdot P_{21}}}=\frac{2P_{21}\dot{P_{21}}}{2\sqrt{P_{21} \cdot P_{21}}} = 0 $$ 那么可以知道 $$ \dot{C}(P_{21}):P_{21}\dot{P_{21}}=(P_1 - P_2)(\dot{P_1}-\dot{P_2})=0 \tag{*} $$ 由于 $$ \dot{P_i} = v_i + \omega_i \times r_i $$ （$\dot{P_i}$是位置的导数也就是速度，$v_i$是物体本身速度，$\omega_i \times r_i$是旋转的线速度)，所以我们得到： $$ \dot{C}(v_1,q_1,v_2,q_2):(P_1-P_2)\cdot(v_1 + \omega_1 \times r_1 - v_2 - \omega_2 \times r_2) = 0 $$ 把里面的东西进行移项(注：使用了混合积定律$A\cdot (B\times C)=C\cdot (A\times B)=B\cdot (C\times A)$)，得到： $$ (P_1 - P_2)\cdot v_1 + (r_1 \times (P_1 - P_2)) \cdot \omega_1 - (P_1 - P_2)\cdot v_2 + (r_2 \times (P_1 - P_2)) \cdot \omega_2 = \begin{bmatrix} (P_1 - P_2) \\ (r_1 \times (P_1 - P_2)) \\ -(P_1 - P_2) \\ -(r_2 \times (P_1 - P_2)) \end{bmatrix}^T \begin{bmatrix} v_1 \\ \omega_1 \\ v_2 \\ \omega_2 \end{bmatrix} = J_cv = 0 $$ 这里的$J_c$被称为Jacobian。$v$则是一个囊括了$P_1,P_2$的线速度，角速度的矩阵。$\lambda$则被称为拉格朗日乘子( Lagrange multiplier)。因为$J_c\cdot v =0$，所以$J_c$一定垂直于$v_1$($v_2$)，并且从$P_1$指向$P_2$($P_2$指向$P_1$)。

这里，$*$式中的$P_1 - P_2$被称为约束轴(constraint axis)，$\dot{P_1} - \dot{P_2}$则是两者的相对速度。这里将相对速度投影到约束轴上来看约束轴到底能多快地被破坏。而这个方程等于0则说明我们希望最后在约束轴上的相对速度保持不变，以此来保持约束不被破坏：

约束轴

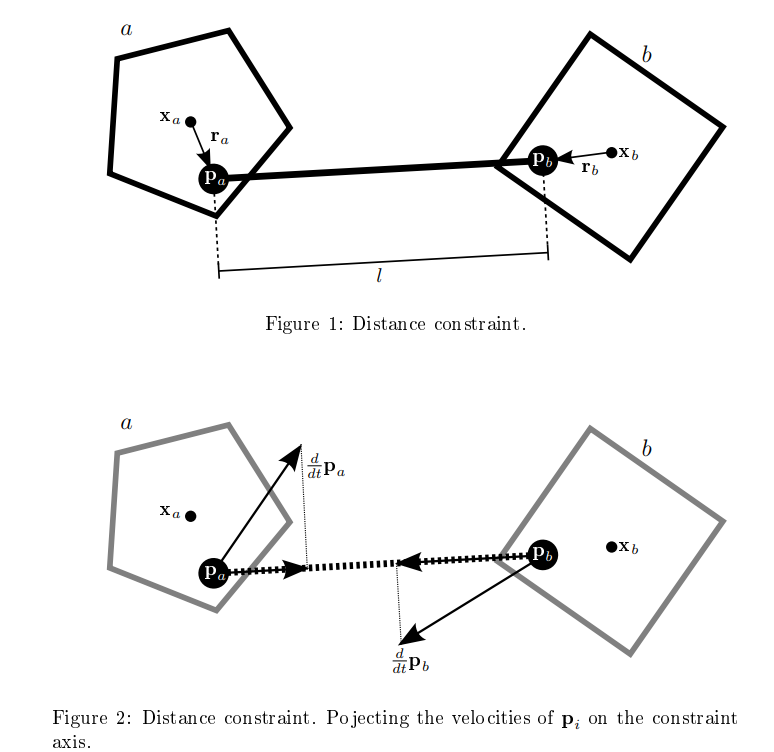
加入$\beta$

就算物体满足了约束$C(x, y)=0$，他也没办法将物体恢复到正确的位置上（我们仅仅是解出这个方程而已，物体的位置仍然没变）。所以需要有一个速度给物体拉回去，那么$J_c$方向上的就不应该是0。那么让我们添加一个$J_c$方向上的速度$v_2$： $$ J_c \cdot (v +v_2) = J_c \cdot v +J_c \cdot v_2 = 0 $$ 这里$J_c \cdot v_2$一定不是0，令其为$\epsilon$，得到最后的式子： $$ J_c \cdot (v +v_2) = J_c \cdot v + \epsilon = 0 $$ $\epsilon$在这里的理解是当前速度到约束下速度之间的误差。

那么这个$\epsilon$在我们的连杆系统下到底是多少呢？要想将物体拉回去，物体的速度应该是： $$ v = -\frac{\lVert P_{12} \rVert - l}{\Delta t} $$ 但你不能真的使用这个速度，因为在实际编码中（下面说到的$SI$求解器中）会在一帧内使用多次这个速度。所以我们需要适当地降低这个速度。提供一个$\beta \in (0, 1)$来减弱$v$： $$ \epsilon = -\frac{\lVert P_{12} \rVert - l}{\Delta t} \beta $$ 这个方法一般被称为Baumgarte stabilization，他的通用表示和约束方程$C$有关： $$ \epsilon = -\frac{C}{\Delta t} \beta $$

一般来说，为了之后求解方便，会将$\epsilon$移动到等号右边去（我们下面也按照这个公式推导）： $$ J_c\cdot v = \epsilon \ \epsilon = \frac{C}{\Delta{t}} \beta, \beta \in [0, 1] $$

求解最后应施加的力

最后我们来求解整个约束应该施加给物体的力。

在曲线运动下，只有一个约束力$F_c$从$P_1$指向$P_2$。巧了，我们的$J_c$也是这个方向，那么显然有一个常数$\lambda$，使得 $$ F_c = \lambda J_c^T \tag{1} $$ （注：为什么是$J_c^T$？，因为$J_c$是行向量，我们这里所有的向量表示都是列向量）由牛顿第二定律，又有： $$ F = M\dot{V}\ F_c +F_{ext} = M\dot{V} \tag{2} $$ $F_{ext}$是除了约束力之外的力。$\dot{V}$在这里是物体线速度，角速度的矩阵导数： $$ \dot{V} = \begin{bmatrix} v_1 \\ \omega_1 \\ v_2 \\ \omega_2 \end{bmatrix}' $$ 注意，因为$\dot{V}$中存在角速度$\omega_i$，所以$F_c$和$F_{ext}$其实是表示两种力——力和力矩： $$ F = \begin{bmatrix} F_1 \\ \tau_1 \\ F_2 \\ \tau_2 \end{bmatrix} $$ 那么有： $$ \lambda J_c^T = M\dot{V} \\ \lambda J_c^T + F_{ext} = M\dot{V} $$ 矩阵$M$则是和线速度，角速度对应的质量矩阵： $$ M=\begin{bmatrix} m_1 & 0 & 0 & 0 \\ 0 & I_1 & 0 & 0 \\ 0 & 0 & m_2 & 0 \\ 0 & 0 & 0 & I_2 \end{bmatrix} $$ 其中$m_i$是质量， $I_i$是转动惯量。这四个元素分别对应$\dot{V}$里的线速度和角速度。

那么$\dot{V}$如何解？假设两帧之间时间极短，那么可以用平均速度代替导数： $$ \dot{V}=\frac{V_{new} - V_{old}}{\Delta t} $$ 其中$V_{new}$是下一帧应该有的速度，$V_{old}$是这一帧的速度。根据“加入$\beta$”一节，我们知道$J_c\cdot V_{new} = \epsilon$，所以有： $$ \Delta{t} \dot{V} = V_{new} - V_{old} \\ J_c\Delta{t} \dot{V} = J_c\cdot V_{new} - J_c\cdot V_{old} \\ J_c\cdot \dot{V} \Delta{t} + J_c\cdot V_{old} = \epsilon \\ \tag{3} $$ 然后由$1$，$2$式可得$\dot{V}$： $$ \lambda J_c^T + F_{ext} = M\dot{V} \\ \dot{V} = M^{-1}(\lambda J_c^T + F_{ext}) $$ 然后把这个式子带入$3$式： $$ J_c\cdot V_{old} + J_cM^{-1}(\lambda J_c^T + F_{ext})\Delta{t} = \epsilon \\ J_cM^{-1}J^{T}\lambda = \frac{\epsilon}{\Delta{t}}-J_c(\frac{V_{old}}{\Delta{t}}+M^{-1}F_{ext}) $$ 那么令： $$ A = J_cM^{-1}J^{T} \\ b = \frac{\epsilon}{\Delta{t}}-J_c(\frac{V_{old}}{\Delta{t}}+M^{-1}F_{ext}) $$ 这样问题就变成了求解函数： $$ A\lambda = b $$ 注意：实际求解的时候$M^{-1}$其实就是： $$ M^{-1} =\begin{bmatrix} 1/m_1 & 0 & 0 & 0 \\ 0 & 1/I_1 & 0 & 0 \\ 0 & 0 & 1/m_2 & 0 \\ 0 & 0 & 0 & 1/I_2 \end{bmatrix} $$ 不需要真的按公式计算逆矩阵（什么，你的质量是0？那给个1就行了）。

在计算机中，解这个方程可以用Gauss–Seidel方法或者Jacobi等方法。我看的所有参考中都是用Gauss-Seidel算法解的，所以就用这个方法解吧。

SI(Sequential-Impulse)求解器

使用上述方法求解的求解器称为SI求解器：

首先，我们的公式是在圆周运动下推导的。而任意曲线运动在某一时刻都可以视为圆周运动，所以这个推导过程是可以在每一帧使用的。

其次，我们在算$\dot{V}$的时候说“在时间很小的情况下可以用近似”，所以增加物理引擎的精度的一个方法就是将一份时间拆成多段迭代计算，段数越多越准。

具体做法是：

将所有非约束力全部应用在物体上，得到一个猜测的速度
依次计算所有$\lambda$并将所有约束力应用在物体上，用来矫正速度
使用最后的速度来更新物体位置

上面的第二步在一帧内要一直做，直到满足当中一个条件：

没有约束力产生或约束力特别小
达到了一定步数（避免死循环或时间过长）

约束类型

距离约束（Distance Constraint）

这种约束需要两个物体总是保持一定距离，比如我们上面举的连杆的例子。这里再稍稍拓宽一点：之前都是将$P_1$和$P_2$视为质点。这里如果加上刚体的话$P_1 - P_2$则是连杆两端的距离：

连杆约束

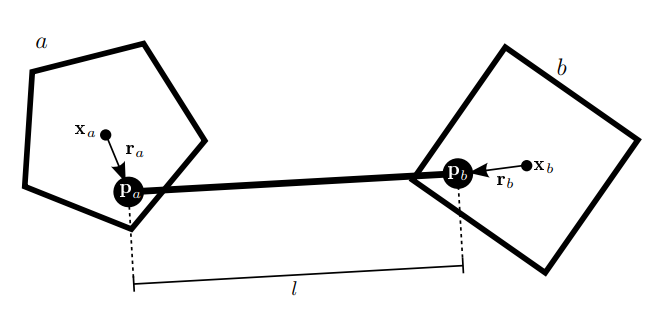
接触约束（Contact Constraint）

这种约束是当物体产生接触时，将两个物体分离开的约束。

接触约束

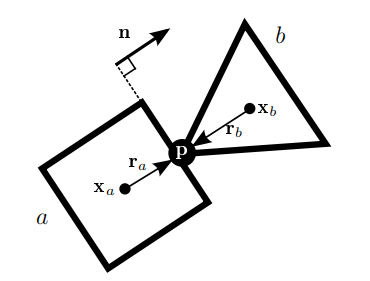
其中$P_1 - P_2$被替换成接触面的法向量。那么$J_c$变为： $$ J_c = \begin{bmatrix} -n \\ -(r_a \times n) \\ n \\ (r_b \times n) \end{bmatrix}^T $$

那这里的恢复向量就是： $$ v = \frac{d}{\Delta t}bias $$ $d$是相交深度。

如果物体b是静态物体（无论怎样都不移动的），$J_c$可变为： $$ J_c = \begin{bmatrix} -n \\ -(r_a \times n) \\ 0 \\ 0 \end{bmatrix}^T $$

A的求解细节

我在看Box2D-Lite源码的时候发现了他对A的求解方法：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


void Arbiter::PreStep(float inv_dt)
{
	const float k_allowedPenetration = 0.01f;
	float k_biasFactor = World::positionCorrection ? 0.2f : 0.0f;

	for (int i = 0; i < numContacts; ++i)
	{
		Contact* c = contacts + i;

		Vec2 r1 = c->position - body1->position;
		Vec2 r2 = c->position - body2->position;

		// Precompute normal mass, tangent mass, and bias.
		float rn1 = Dot(r1, c->normal);
		float rn2 = Dot(r2, c->normal);
		float kNormal = body1->invMass + body2->invMass;	// kNormal就是A
		kNormal += body1->invI * (Dot(r1, r1) - rn1 * rn1) + body2->invI * (Dot(r2, r2) - rn2 * rn2);
		c->massNormal = 1.0f / kNormal;

        ...
    }

看17行，这里没有用叉乘算$r_a \times n$，因为$r_a \times n = \lVert r_a \rVert \sin{<r_a, n>}$，所以他算出三角形斜边$\lVert r_a \rVert$和临边$r_a \cdot n$然后用三角函数直接解出来了，没有用叉乘（代码中是Dot(r1, r1) - rn1 *rn1）。