本文介绍了蒙特卡洛算法,重要性采样,拟蒙特卡洛算法。
蒙特卡洛算法
蒙特卡洛算法是一种使用概率方法计算定积分的方法。
概率论回顾
首先回顾一些概率论知识并定义一些符号:
概率密度函数(Probability Density Function, PDF):
对任意的随机变量$X_i$,其pdf是其在这一点的概率的函数:
$$ p_i = pdf(X_i) $$
比如投骰子,记$X_i$为投出$i$点的概率,那么有:
| $pdf(X_i)$ | $X_i$ |
|---|---|
| $\frac{1}{6}$ | 1 |
| $\frac{1}{6}$ | 2 |
| $\frac{1}{6}$ | 3 |
| $\frac{1}{6}$ | 4 |
| $\frac{1}{6}$ | 5 |
| $\frac{1}{6}$ | 6 |
(一般在离散情况下我们称概率密度函数为分布率)
累积分布函数(或简称分布函数)(Cumulative Distribution Function, CDF):
其定义如下:
$$ cdf(x) = \int_{-\inf}^x pdf(x) \text{d} x $$
显然存在如下性质:
$$ cdf(x) \ge 0 $$
$$ \lim_{x\rightarrow\inf} cdf(x) = 1 $$
然后是伯努利大数定律:
设多个随机变量$X_1,X_2,...X_i$独立同分布,$f_A$是这n次独立重复实现中事件A发生的概率,$p$是事件A在每次实验中发生的概率,则对于任意的$\epsilon \lt 0$,有:
$$ \lim_{n\rightarrow \inf}P{|\frac{f_A}{n} - p)| \lt \epsilon} = 1 $$
也就是说,只要我们独立重复试验做的次数够多,我们就可以用A事件成功的频率去逼近A事件的概率。这也是大部分教材上对概率最初的定义。
蒙特卡洛算法初步理解
蒙特卡洛算法就是基于伯努利大数定律而产生的算法,回想经典的求圆面积的算法,有一种投针法:
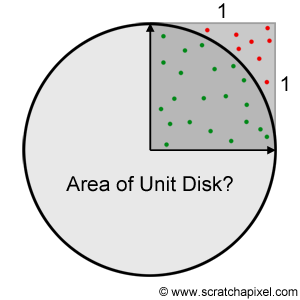
对于半径为r圆,我们画出其最小的AABB包围盒,然后在包围盒中不停地随机投针,记总共投针的次数为$n$,针在圆内的次数为$A$,那么在我们投了无数次之后,我们就可以得到圆的面积:
$$ S = \frac{A}{n} 4r^2 $$
其中$4r^2$为AABB的面积。
这里的投针法其实就是蒙特卡洛算法,那么对于任意的函数$f(x)$,其积分记作$F(x) = \int_a^b f(x)\text{d}x$,根据定积分的定义,$F(x)$其实是$f(x)$围绕x轴的面积:
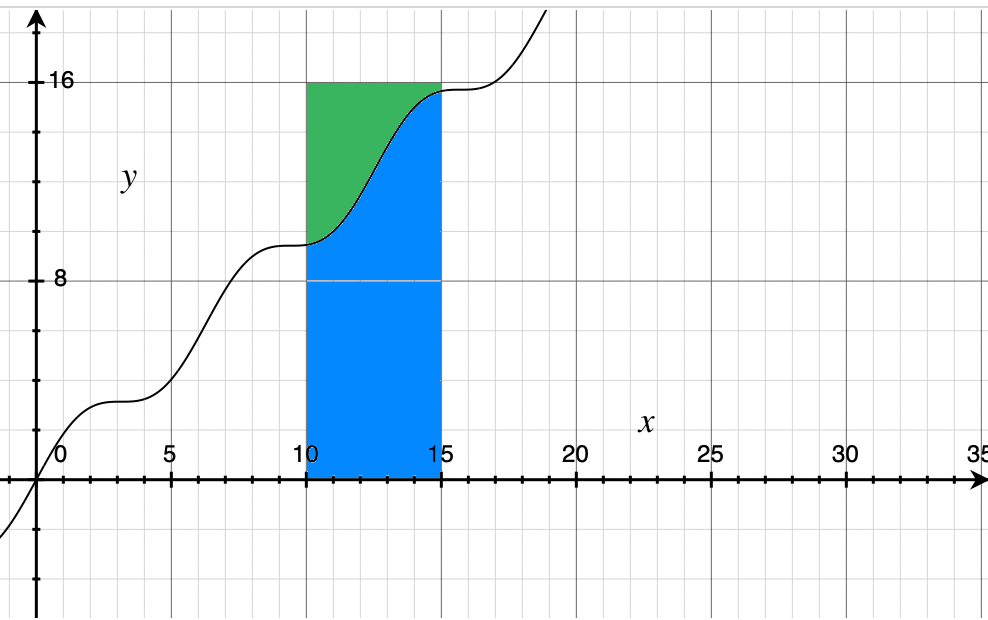
比如我们这里要计算此函数在区间$[10, 15]$上的积分,我们只需要不停地对蓝色和绿色的区域进行投点,然后记录点落在蓝色区域内的数量,最后做比就可以得到积分的估计值。
当$X_i$以某种分布进行采样时,蒙特卡洛算法变成如下公式:
$$ F(x) = \frac{1}{n}\sum_{k = 1}^n\frac{f(X_k)}{pdf(X_k)} $$
比如你使用均匀分布进行采样,均匀分布的pdf为:
$$ \begin{cases} pdf(x) = \frac{1}{b - a}, & x\in [a, b] \ 0, & 其他 \end{cases} $$
那么蒙特卡洛公式就是:
$$ F(x) = \frac{b - a}{n}\sum_{k = 1}^{n}f(X_k) $$
如何从概率分布得到随机数,可以看visualgmq-随机数生成算法
重要性采样
对于某些函数,比如
$$ \begin{cases} 99.01, &x \in [0, 0.01) \ 0.01, & x \in [0.01, 1] \end{cases} $$
他的图像是这样:
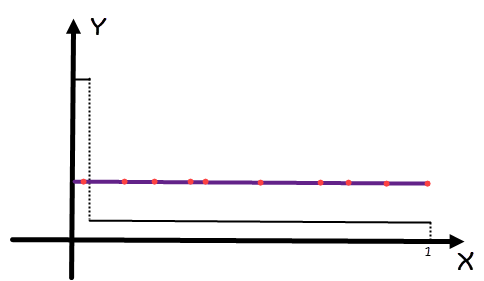
如果我们要算其[0, 0.5]的积分,我们使用均匀分布的话,很显然有大部分的点其实都不会打到函数内部,所以求出来的值就会偏小。
重要性采样就是需要根据函数的形状,来确定自己的分布函数,以便更好地得到最后的结果。选择更加贴切的分布函数可以更快地得到误差更小的结果。
理论上,对于任意的被积函数,其最优概率密度函数为:
$$ pdf(x) = \frac{|f(x)|}{\int f(x) \text{d}x} $$
但显然这没什么意义,因为公式中有我们要求的$f(x)$的积分。
拟蒙特卡洛算法
拟蒙特卡洛算法的核心是不使用随机数,而是使用低差异序列。优点是积分的收敛速度更快,在同样的采样数下,误差更小。
由于伪随机数可能产生集聚的情况,所以我们首先可以想到将积分区间平均分成多份,然后在每一份中使用一些随机数进行采样。这种方法就叫分层采样。
而低差异序列则是不需要对采样空间进行手动分割,就可以同时具备空间平均性和随机性这两个特点。
在介绍这些方法前,必须定义什么是差异:
设$P={x_1, ..., x_n}$是一组位于$[0, 1]^s$下的点集,差异可以定义为:
$$ D_n(P) = \sup_{B \in J}{|\frac{A(N)}{n} -\lambda_s(B)|} $$
其中,s是维度,J是整个区域,B是在J中任取的一个区域,$A(B)$是在B区域内点的数量,$n$是整个区域内点的数量,$\lambda_s{B}$则是B区域的体积。
这个公式直白点说就是,区域B内的点和整个区域的点的比值越接近B的体积(越聚集在一起),则这些点的差异越小。($\sup$是指一个集合最小的上界)
具体的生成序列的方法有很多:
- Van der Corpu
- Halton
- Hammersley
- Sobol
这里推荐看参考中的后两条。