本文是Games101 RayTracing课程中辐射度量学一章的笔记。
辐射度量学
辐射度量学是一套基于物理的光线理论,虽然只是几个公式,但学习他可以很好地帮助我们理解BRDF,PBR,AO等算法的概念。
基本概念
- Radiant flux: 辐射通量
- intensity:光强度(一般记作$I$)
- irradiance:辐照度
- radiance:辐射度
Radiant Energy和Radiand Flux
Radiant Energy(辐射强度)是电磁辐射在单位面积上的能量,用$Q$表示,单位是焦耳($J$)
Radiant Flux(辐射通量)的定义是:
$$ \Phi = \frac{dQ}{dt} $$
即单位时间内的Radiant Energy。单位是瓦特($W$),或者流明($lm$)。
这个公式可以这样理解,将其变换:
$$ \text{d}Q = \Phi\text{d}t $$
在辐射通量一定的情况下,光发出的能量和时间成正比,这显然符合现实的情况。
Radian Intensity
即辐射强度,指一个光源向周围发射的光强度。定义为:
$$ I(\omega) = \frac{d\Phi}{d\omega} $$
其中$\omega$是Solid Angle(立体角)的单位。
Radian Intensity的单位是坎德拉($cd$)
Solid Angle
是三维空间中对角度的定义。
在二维空间中,我们知道圆的弧长公式是:
$$ l = r\theta $$
那么可以得到角度的定义:
$$ \theta = \frac{l}{r} $$
在三维的球中,也可以如法炮制:
$$ r^2 \omega = S \Rightarrow \omega = \frac{S}{r^2} $$
其中$S$是球对应立体角的面积,$r$则是球的半径。
立体角的单位是steradian(球面度,简记$sterad$)
显然,$\omega \in [0, 4\pi]$。
单位立体角则是在单位球中,对应面积$S$的立体角。
微分立体角则是立体角的微分,可以从球坐标系中算出来:
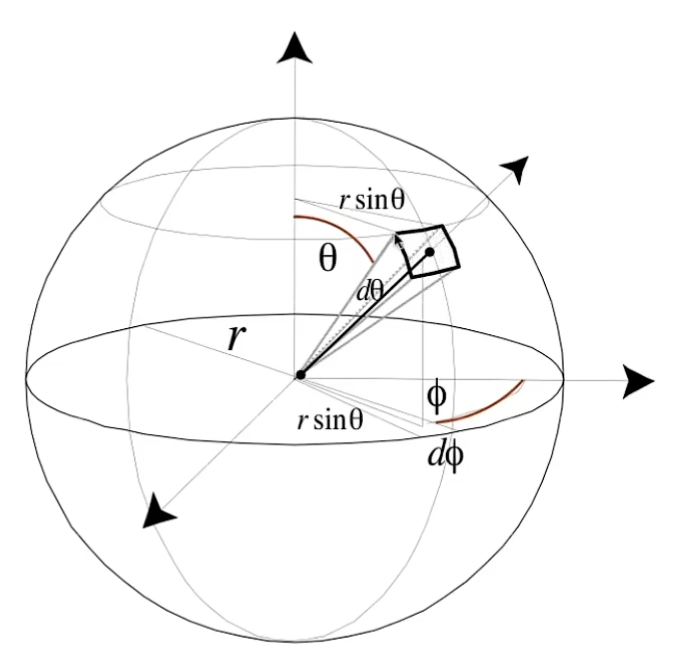
首先算出单位立体角对应的面的面积:
$$ dS = (r\text{d}\theta)(r\sin{\theta}\text{d}\phi) = r^2\sin{\theta}\text{d}\theta \text{d} \phi $$
那么有
$$ \frac{\text{d}S}{r^2} = \sin{\theta}\text{d}\theta\text{d}\phi = \text{d}\omega $$
你可以反过来验证:
$$ \int_S \sin{\theta}\text{d}\theta\text{d}\phi = \int^{2\pi}_0 \int^{\pi}_0\sin{\theta}\text{d}\theta\text{d}\phi = 4\pi $$
这样通过公式
$$ I = \frac{\text{d}\Phi}{\text{d}\omega} $$
可以得到
$$ \text{d}\Phi = I\text{d}\omega \Rightarrow \Phi = \int_{S^2} I\text{d}\omega $$
其中$S^2$是指整个光源所在的球面的面积。
Irradiance
即辐照度,是指单位面积上的辐射通量:
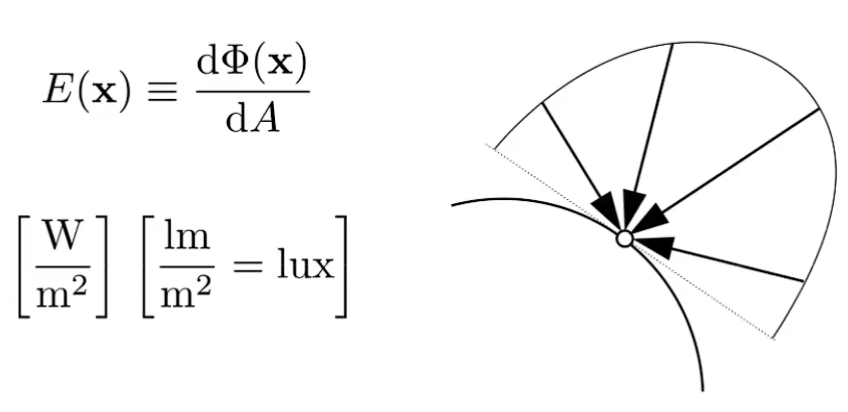
$$ E(x) = \frac{\text{d}\Phi(x)}{\text{d}S} $$
单位是$lux$
注意Irradiance和Radiant Intensity的区别。Radiant Intensity是度量光源发出光强度的量,而Irradiance是某点接收光辐射的量。
Radiance
即辐射度(或辐射),是描述光在环境中分布的基本量。Radiance和光的方向有关。
Radiance的定义如下:
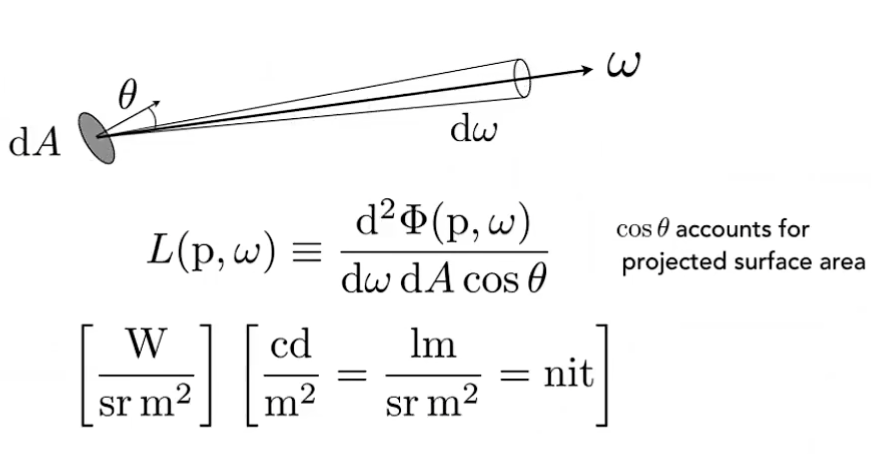
$$ L(p,\omega) = \frac{\partial^2{\Phi(p, \omega)}}{\partial{\omega}\partial{S\cos{\theta}}} $$
单位是尼特($nit$)。
这里$p$是辐射到的点,$\omega$是立体角,$S$是辐射到这一点的面积,$\cos\theta$是这一点所在面的法向量和光线的夹角。
这里的Radiance是总体的定义,我们也可以对入射和出射光定义,分别是光源发出的Radiance(Exiting Radiance)和接收的Radiance(Incident Radiance)。
Exiting Radiance使用Radiant Intensity定义,根据前面对Radiant Intensity的定义,可以将公式变化为:
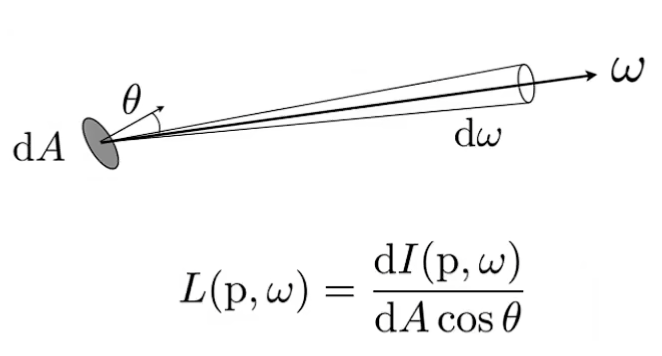
$$ L(p,\omega) = \frac{\partial{I(p, \omega)}}{\partial{\omega}\partial{S\cos{\theta}}} $$
Incident Radiance使用Irradiance定义,根据Irradiance的定义,可以将公式化简为:
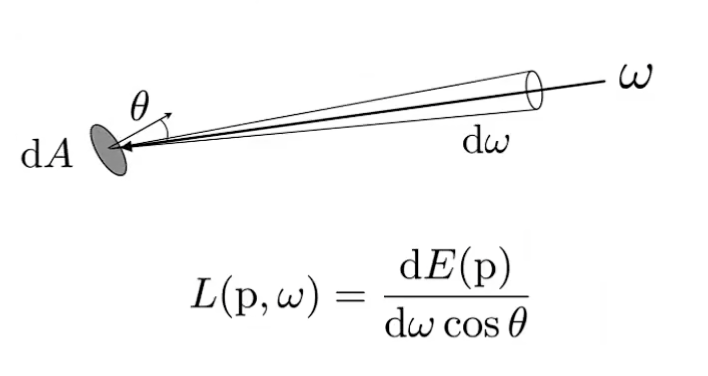
$$ L(p,\omega) = \frac{\text{d}{E(p, \omega)}}{\text{d}{\omega}\cos{\theta}} $$
Iradiance 和 Radiance的联系
通过对Radiance的定义可以得到:
$$ L(p, \omega) = \frac{\text{d}E(p)}{\text{d}\omega \cos{\theta}} \Rightarrow \text{d}E(p) = L(p, \omega)\text{d}\omega \cos{\theta} $$
即
$$ E(p) = \int L(p, \omega) \cos{\theta} \text{d}\omega $$
显然,irradiance只是在radiance上增加了方向,而这个公式则说明了,某一点所受的irradiance的总量为其半球面上垂直于该面的radiance总和:
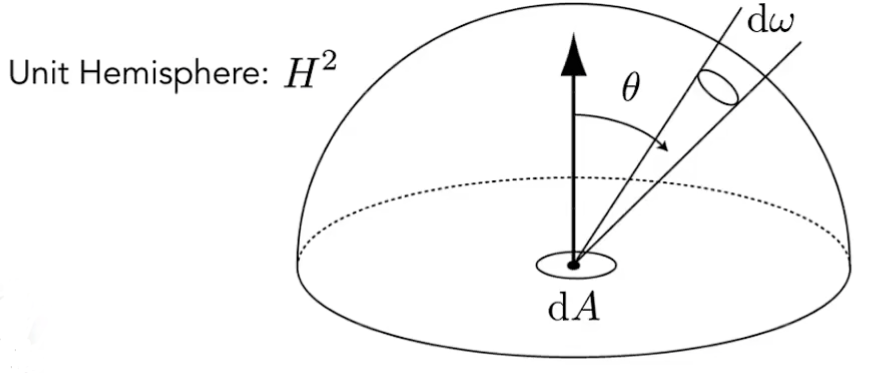
之所以是半球面,是因为从面的底部照射的光不应该产生任何光照效果。