本文描述了3D空间中的旋转，包括使用欧拉角旋转，四元数旋转，绕坐标轴轴旋转，绕旋转轴旋转以及四元数插值。
欧拉角
欧拉角是很直白的旋转方式，其思想就是先绕x轴旋转，再绕y轴旋转，再绕z轴旋转（这里x,y,z的顺序不是固定的）。这样的想法让我们将3D空间的旋转拆分为三个2D平面旋转的组合：
$$ EulerRotateMat = \ \begin{bmatrix} \cos{\gamma} & -\sin{\gamma} & 0 & 0 \ \sin{\gamma} & \cos{\gamma} & 0 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1 \ \end{bmatrix}\begin{bmatrix} \cos{\beta} & 0 & \sin{\beta} & 0 \ 0 & 1 & 0 & 0 \ -\sin{\beta} & 0 & \cos{\beta} & 0 \ 0 & 0 & 0 & 1\ \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & 0 \ 0 & \cos{\alpha} & -\sin{\alpha} & 0 \ 0 & \sin{\alpha} & \cos{\alpha} & 0 \ 0 & 0 & 0 & 1 \end{bmatrix} $$ 欧拉角的优点是很简洁直观，缺点是由很多问题，这里有一个视频展示了使用欧拉角带来的这些问题（14:20 ~ 17:43）。
万向节死锁问题
万向节死锁仅发生在动态旋转中。
旋转分为两种：静态旋转，动态旋转。静态旋转是指每次旋转的旋转轴都是世界坐标系下的坐标轴（即绕x轴即绕$(1, 0, 0)$，绕y轴即绕$(0, 1, 0)$，z轴则是$(0, 0, 1)$）。而动态旋转则是按照旋转体当前的轴，即旋转体的局部坐标系的轴。
绕任意轴旋转的矩阵
有了欧拉角，我们可以推导出绕任意轴旋转$\theta$角的方法：
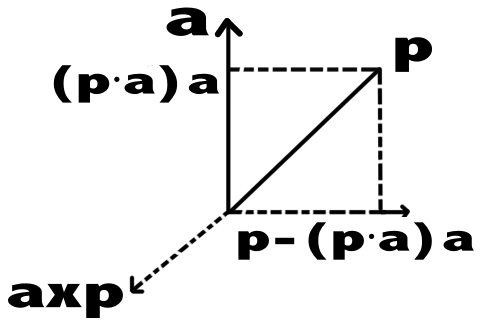假设$\vec{a}$为旋转轴的单位向量，$p$是旋转的点，那么首先首先$\vec{p}$在$\vec{a}$上的投影为
$$ proj_a{p} = (p\cdot a)a $$ 那么与a，p在同一平面内，且垂直于a的轴为
$$ p - proj_ap = p - (p\cdot a)a $$
然后我们再用叉乘求得垂直于a，(p·a)a的轴：
$$ a \times p $$ 因为和$a$平行的分量$proj_ap$不受旋转影响，那么这个问题就变成在$a\times p$和$p - (p\cdot a)a$平面中对p的垂直分量进行旋转。这是典型的2D旋转，可以很容易得到：
$$ p^{'}_h = [p - (p\cdot a)a]\cos{\theta} + (a\times p)\sin{\theta} $$
然后我们再加上$proj_ap$即可：
$$ p^{'} = p^{'}_v + p^{'}_h = proj_ap + p^{'}_h = (a\cdot p)a + [p - (p\cdot a)a]\cos{\theta} + (a\times p)\sin{\theta} $$
化简得
$$ p^{'} = p\cos{\theta} + (a\times p)\sin{\theta} +(1-\cos{\theta})(a\cdot p)a $$
接下来将其变为矩阵形式。
$proj_qp$的矩阵形式为
$$ \begin{bmatrix} q_x^2 & q_xq_y & q_xq_z \ q_xq_y & q_y^2 & q_yq_z \ q_xq_z & q_yq_z & q_z^2 \ \end{bmatrix}
\begin{bmatrix} p_x \ p_y \ p_z \ \end{bmatrix}
\frac{1}{|q|^2} $$
而$p\times q$的矩阵表示形式为：
$$ p \times q = \begin{bmatrix} 0 & -p_z & p_y \ p_z & 0 & -p_x \ -p_y & p_x & 0 \ \end{bmatrix}
\begin{bmatrix} q_x \ q_y \ q_z \ \end{bmatrix} $$
我们可以用如上的两个公式将绕轴旋转公式表示成矩阵形式，设$c = \cos{\theta}$，$s = \sin{\theta}$
$$ \begin{bmatrix} c+(1-c)a_x^2 & (1-c)a_xa_y - sa_z & (1-c)a_xa_z + sa_y \ (1-c)a_xa_y + sa_z & c+(1-c)a_y^2 & (1-c)a_ya_z - sa_x \ (1-c)a_xa_z - s a_y & (1-c)a_ya_z + sa_x & c + (1-c)a_z^2 \ \end{bmatrix} $$
四元数
四元数可以说是完美解决3D空间旋转的一个绝佳办法，与欧拉角相比只需要多一些数学知识。它由哈密顿发现。当时哈密顿一直在寻找三维空间中的复数（即带有两个虚数单位的复数-三元数），但在经过一座桥时，他突然明白没有办法得到三元数，而是应该再升高一个维度，得到四元数。他当时就将它脑中所想的四元数公式刻在桥上，四元数就诞生了。
基本公式
四元数通俗来说就是有三个虚数单位的复数，回想复数的定义：
$$ \begin{aligned} p & = a\pmb{i} + b \ \pmb{i}^2 & = -1 \ \end{aligned} $$
而四元数则是有四个虚数单位的复数：
$$ \begin{aligned} p = a\pmb{i} + b\pmb{j} + c\pmb{k} + d \ \pmb{i}^2 = \pmb{j}^2 = \pmb{k}^2 = -1 \ \pmb{ij} = \pm{k}, \pmb{jk} = \pmb{i}, \pmb{ki} = \pmb{j} \ \pmb{ji} = \pmb{k}, \pmb{kj} = -\pmb{i}, \pmb{ik} = -\pmb{j} \ \end{aligned} $$
后面的几条规则可以这样记忆：想象i,j,k分别是3D空间中的x,y,z轴的单位向量，他们的乘积结果总是剩下那个轴的所代表的的虚数单位，而结果的符号则由右手定则确定。而相同虚数单位和自己的乘积总是-1。
一般将四元数记为：
$$ q = \begin{bmatrix} \pmb{q}_v & q_s \end{bmatrix} $$ 其中矢量部分为$\pmb{q}_v = x\pmb{i} + y\pmb{j} + z\pmb{k}$，而标量部分为$q_s = w$
四元数比欧拉角更优秀的地方在于：
- 没有万向节死锁问题
- 只需要存储四个浮点数，比矩阵表示更加简单
- 四元数求逆，串联等操作比矩阵更加高效
四元数和复数有着很多共通特性，比如，任意一个复数$x\pmb{i}+y$可以在复平面内表示一个点$(x, y)$，而四元数作为四维空间的负数，其$x\pmb{i}+y\pmb{j}+z\pmb{k}+w$表示的则是四维空间中的一个点$(x, y, z, w)$。
再比如，对于复数，我们乘上一个虚数单位其实是将其对应点逆时针旋转了90度。同理，在四元数中乘上某一轴所代表的虚数单位，则是表示绕此轴逆时针旋转90度。
四元数的乘法计算规则如下：
$$ \begin{aligned} p & = \begin{bmatrix}\pmb{p}_v & p_s\end{bmatrix} \ q & = \begin{bmatrix}\pmb{q}_v & q_s\end{bmatrix} \ p*q & = \begin{bmatrix}(p_s\pmb{q}_v + q_s\pmb{p}_v + \pmb{p}_v \times \pmb{q}_v) & (p_sq_s - \pmb{p}_v \pmb{q}_v)\end{bmatrix} \end{aligned} $$ 就是用乘法结合律拆开了计算。这叫做格拉斯曼积。其中$\pmb{p}_v\times\pmb{q}_v$是将p，q的虚部看做向量进行叉积，而$\pmb{p}_v\pmb{q}_v$则是其对应向量的点积。
四元数有很多种乘法，但是格拉斯曼积是最通用的形式。
四元数满足：
- 封闭性：四元数的四则运算结果还是四元数
- 结合律：$(pq)r = p(qr)$
四元数的单位元素和逆元素：
- 单位元素：$(1, 0, 0, 0)$，任何四元数乘上单位元素都等于自身。
- 逆元素：$q^{-1} = \frac{q^*}{|q|^2}$，任何四元数和其逆相乘为单位元素。
其中$|q|^2$代表其模的平方（即$x^2 + y^2 + z^2 + w^2$），$q^{-1}$则是$q$的共轭（和复数共轭类似：$q^{-1} = w -xi - yj - zk$）。 共轭和逆还有如下性质：：
$$ \begin{aligned} q^q = qq^ = |q|^2 \ (qp)^* = p^q^ \ (qp)^{-1} = p^{-1}q^{-1} \end{aligned} $$
四元数表示旋转
只有单位四元数才能表示旋转。因为根据四元数的几何意义，$\pmb{q}_v = x\pmb{i}+y\pmb{j}+k\pmb{k}$代表着3维空间中的三条虚数轴，而$q_s = w$则代表第四维度中垂直于三维的一条轴。
第四维度的轴对我们来说没什么用，我们只需要用到三维的虚数轴就可以了。
首先要将单位四元数视为旋转矢量，其公式如下：
$$ q = \begin{bmatrix}\pmb{q}_v & q_s\end{bmatrix} = \begin{bmatrix}\vec{a}\sin{\frac{\theta}{2}} & \cos{\frac{\theta}{2}}\end{bmatrix} = \begin{bmatrix} a_x\sin{\frac{\theta}{2}} \ a_y\sin{\frac{\theta}{2}} \ a_z\sin{\frac{\theta}{2}} \ \cos{\frac{\theta}{2}} \end{bmatrix} $$ $\vec{a}$是旋转轴所在的单位矢量。旋转的方向根据右手定则（前提是你用的是右手系）决定（握住旋转轴，大拇指朝向$\vec{a}$的朝向，四指环绕方向即为旋转方向。
然后再用旋转矢量去旋转物体：
$$ v^{'} = qvq^{-1} = qvq^* $$ 由于q是单位矢量，由公式$q^{-1} = \frac{q^*}{|q|}$可知q的逆和其共轭是相等的。
这里需要将点$v = [x\ y\ z\ w]$也视为四元数$w + x\pmb{i} + y\pmb{j} + z\pmb{k}$。
这个公式可以化简成不将$v$转化成四元数的版本：
$$ \pmb{v^{'}} = \pmb{v} + 2\pmb{q}_v\times(\pmb{q}_v \times \pmb{v} + q_s\pmb{v}) $$ 这里只需要单纯的将$\pmb{v}$视为三维的向量即可，此公式还减少了运算量。
和矩阵类似，旋转也可以串接：
$$ \begin{aligned} q_{net} & = q_3q_2q_1 \ v^{'} & = q_{net}vq_{net}^{-1} = q_3q_2q_1vq_1^{-1}q_2^{-1}q_3^{-1} \end{aligned} $$
四元数的旋转也可以写成对应的矩阵形式，只需要将上面的旋转公式用矩阵形式表示即可：
$$ \pmb{R} = \begin{bmatrix} 1-2y^2-2z^2 & 2xy + 2zw & 2xy - 2yw \ 2xy - 2zw & 1-2x^2 - 2z^2 & 2yz + 2xw \ 2xz + 2yw & 2yz - 2xw & 1-2x^2 - 2y^2 \ \end{bmatrix} $$
用于旋转的四元数的存储优化
一般来说，四元数需要四个float变量来存储，但是由于用于旋转的四元数必须是单位长度的（$x^2+y^2+z^2+w^2 = 1$）,所以我们其实可以只存储三个元素，然后另一个元素通过计算得到：
$$ w = \pm \sqrt{x^2 + y^2 + z^2} $$ 这里还有一个问题是无法确定w的符号。我们可以利用四元数在旋转时q和-q效果一样这个特性，看到w为负数时直接存储$-\pmb{q}_v$即可。这样我们可以默认重现的w一定是正的。
四元数旋转的线性插值
直接对四元数进行插值即可，假设要从$q_a$旋转到$q_b$，那么从a到b之间$\beta$百分点的中间旋转$q_{LERP}$为：
$$ q_{LERP} = LERP(q_a, q_b, \beta) = \frac{(1-\beta)q_a + \beta q_b}{|(1-\beta)q_a + \beta q_b|} = normalize( \begin{bmatrix} (1-\beta)q_{a_x} + \beta q_{b_x} \ (1-\beta)q_{a_y} + \beta q_{b_y} \ (1-\beta)q_{a_z} + \beta q_{b_z} \ (1-\beta)q_{a_w} + \beta q_{b_w} \ \end{bmatrix}) $$ 需要注意的是线性插值可能会改变四元数的长度，所以最后要归一化四元数。
这个公式存在一定问题，因为四元数其实表示四维空间中的球体，上面的公式是在超球的弦上插值，这会导致当$\beta$以恒定速率改变时，旋转却并非以很定角速率进行。我们需要在超球面上进行插值才可以：
$$ SLERP(q_a, q_b, \beta) = w_aq_a + w_pq_p $$ 其中
$$ \begin{aligned} w_a & = \frac{\sin{(1 - \beta)}\theta}{\sin{\theta}} \ w_p & = \frac{\sin{\beta \theta}}{\sin{\theta}} \ \end{aligned} $$
参考
四元数-基本概念-知乎 四元数和旋转 四元数和旋转（知乎） 《游戏引擎架构 第二版》