本文是Games101 RayTracing3的笔记,介绍了BRDF和渲染方程。
前置笔记:
BRDF
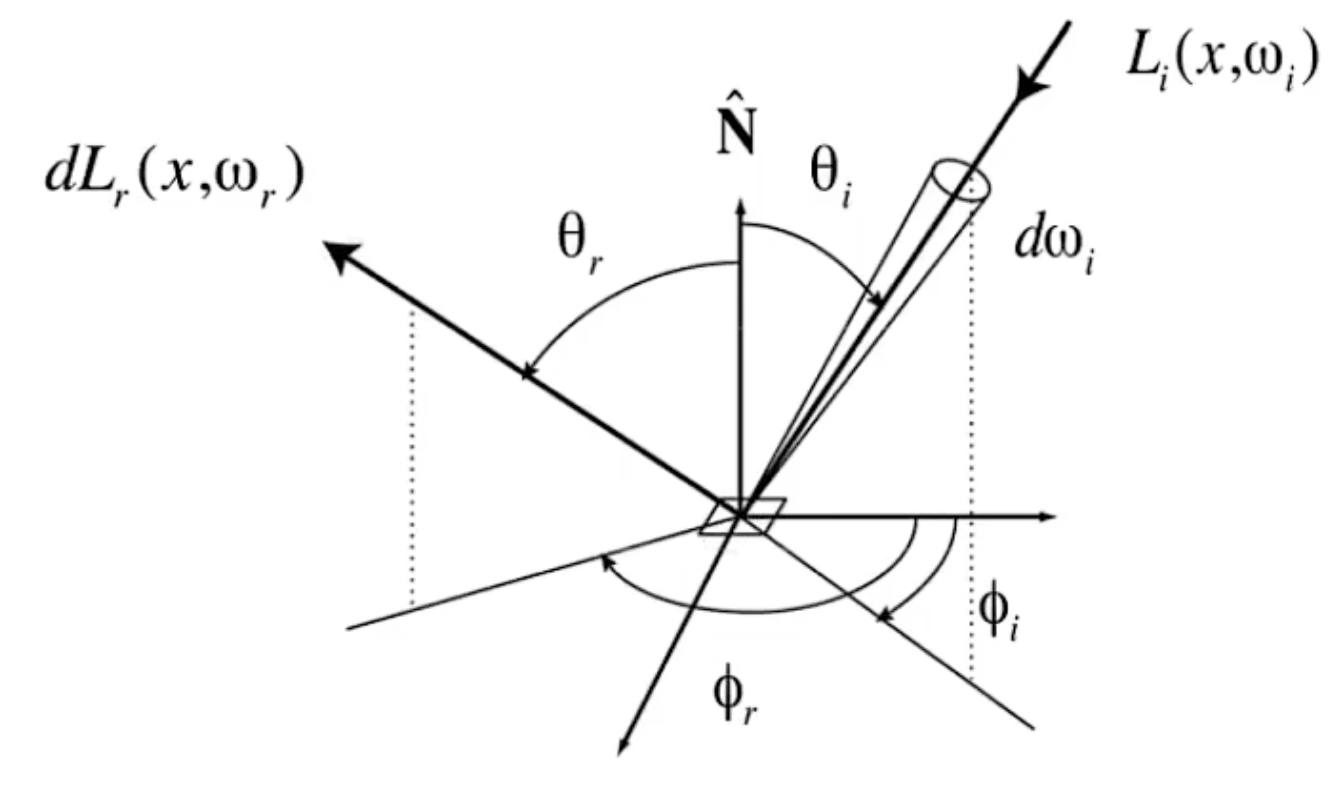
全称是双向反射分布函数。描述的是表面的入射光和反射光之间的关系的函数。定义为:
$$ f_r(\omega_i \rightarrow \omega_r) = \frac{\text{d}L_r(\omega_r)}{\text{d}E_i(\omega_i)} = \frac{\text{d}L_r(\omega_r)}{L_i(\omega_i)\cos{\theta_i}\text{d}\omega_i} $$
BRDF告诉我们,可以从入射的irradiant得到出射的irradiant:
$$ \text{d}L_r(\omega_r) = f_r(\omega_i \rightarrow \omega_r)L_i(\omega_i)\cos{\theta_i}\text{d}\omega_i $$
对上式积分可得:
$$ L_r(\omega_r) = \int_{\Omega^+}f_r(\omega_i \rightarrow \omega_r)L_i(\omega_i)\cos{\theta_i}\text{d}\omega_i $$
这里$\Omega^+$是平面的上半球,也就是说要对所有照射到平面的光源的BFDR乘上入射irradiance乘上$\cos{\theta}$的和,才是平面反射的irradiance。
渲染方程
BRDF很好地告诉了我们平面接收光线后会反射出什么样的光线,但是我们还要考虑平面自发光的情况。将自发光情况加入进去之后就会得到渲染方程:
$$ L_o(p, \omega_o) = L_e(p, \omega_o) + \int_{\Omega^+}f_r(p, \omega_i \rightarrow \omega_r)L_i(p, \omega_i)\vec{n}\omega_i\text{d}\omega_i $$
这里加上了自发光$L_e(p, \omega_o)$,并将$\cos{\theta}$转换为向量点乘$\vec{n}\omega_i$
渲染方程式基本上现代图形学的基础,所有限制在物体表面的光线传播都得满足渲染方程。
接下来需要对渲染方程进行一些化简,好让我们能够从中看出些什么:
首先我们看到,渲染方程中真正的未知量其实是irradiance:
$$ L_o(p, \omega_o),L_i(p, \omega_i) $$
因为物体的自发光$L_e$一定是知道的,光线从哪个角度来和平面的发现也一定是知道的。这里我们假设BRDF也是知道的(后面我们会看到一些光照模型所对应的BRDF函数)。所以只剩下$L_o$和$L_i$不知道。
为了方便,我们定义算子:
$$ I(x) = L_x(p, \omega_x) $$
那么将算子作用在$L_o$和$L_i$上,有
$$ I(o) = L_e(p, \omega_o) + \int_{\Omega^+}I(i)f_r\vec{n}\omega_i\text{d}\omega_i $$
然后将自发光记作$E(o)$,将$f_r\vec{n}\omega_i\text{d}\omega_i$记为$K(o, i)$,那么式子变为:
$$ I(o) = E(o) + \int I(i)K(o, i)\text{d}i $$
然后通过一些奇妙难懂的数学手段(具体是什么我也不清楚,据说是弗雷姆霍得积分方程),可以将式子变为这样:
$$ L = E +KL $$
这里的$L = I(x)$,E为$e(o)$,K为$K(o, i)\text{d}i$。
然后我们可以从这个方程中解出$L$:
$$ \begin{aligned} (I - K)L & = E \ L &= (I - K)^{-1}E \end{aligned} $$
然后对$(I-K)^{-1}$进行泰勒展开(对比$\frac{1}{1-x}$的泰勒展开式)可以得到:
$$ \begin{aligned} L &= (I + K + K^2 + K^3 + ...)E \ L &= E + KE + K^2E + ... \end{aligned} $$
这个式子用通俗语言可以写成这样:
最终反射颜色 = 物体自发光颜色 + 光源发出光线经过第一次反射颜色+ 光源发出光线经过第二次反射颜色 + ...
如果有$L = E$,那说明物体的颜色就是物体本身自发光的颜色。
如果$L = E + KE$,那说明物体的颜色是物体本身的颜色加上光源直接光照的颜色。
以此类推。
其实从原本的渲染方程也可以看出这个结果,不过那个是递归的描述(渲染方程的输入是$L_i(p, \omega_i)$,输出是$L_o(p, \omega_o)$,然后$L_o$又能作为下一个光线到达物体的$L_i$,以此类推)。
渲染方程需要满足能量守恒定律(能量的削弱主要体现在BRDF),那么渲染方程最后会收敛(而不是让场面一片白)。
在离线渲染中需要调整参数以严格满足能量守恒定律。而实时渲染中我们可以近似能量守恒。
BRDF性质
BRDF有如下性质:
- 互换性:$f_r(\omega_i \rightarrow \omega_o) = f_r(\omega_o \rightarrow \omega_i)$,即从入射光线可以得到反射光线,从反射光线可以得到入射光线(这就是九BRDF被称为“双向”反射分布函数的原因)
- $\forall \omega_r: \int f_r(\omega_i \rightarrow \omega_r)\cos{\theta_i} \text{d}\omega_i \le 1$:BRDF满足能量兽痕,总会削减能量。
- $f_r ge 0$:BRDF的结果一定大于等于0(小于0不就是物体吸收光却不发光了嘛,那不成暗物质了)
- 线性性:BRDF可以简单地累加(回想渲染方程中的积分,就是一种累加)从而计算多个光对物体的总影响。