对于Bresenham算法的解释
Bresenham算法#
Bresenham算法是一种绘制直线和曲线的方法。这里主要是介绍如何绘制直线。
带有浮点数的Bresenham算法#
首先我们讨论直线斜率在$[0, 1]$之间的情况：
Bresenham的思想是这样：
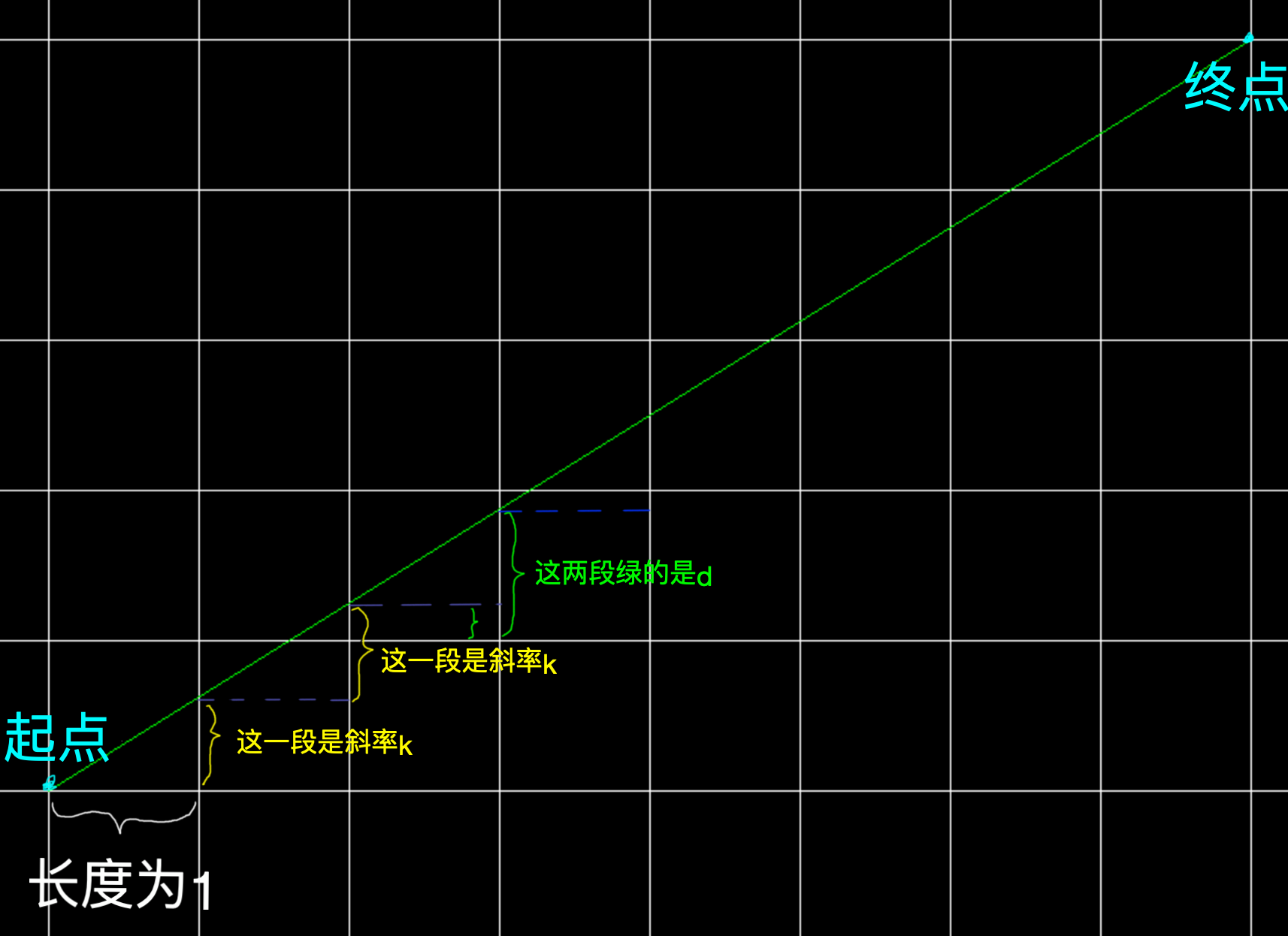
因为计算机是基于像素的，所以将每个像素视为一个格子，并且理想直线从起点到终点，穿过这些格子。
这里由于格子的长度为1，所以黄色所标记的那一段是斜率$k$。
然后定义直线和每个格子的竖直方向交点到下面格子的距离是$d$。
Bresenham的算法思想就是通过判断$d$的值来判断下一个点是取直线上方的点还是下方的点。
如果$d >= 0.5$，那么我们要取直线上方的点。如果$d < 0.5$那么我们要取直线下方的点。
而且显然，在起点处的$d_0 = 0$，然后我们每次迭代的时候令$d_{i+1} = d_i + k$，这样就可以获取到下一个交点到起点所在横线的距离。但是$d$是可能大于1的，所以在$d$大于等于1的时候我们要减去一，这样我们就有了如下的递推式：
$$ \begin{matrix} d_0 = 0 \\ d_{i+1} = d_i + k \\ 如果 d_i >= 1 那么 d_i = d_i - 1 \end{matrix} $$y的变化情况就是这样：
$$ y = \begin{cases} y + 1, d_i >= 0.5 \\ y, d_i < 0.5 \end{cases} $$这样我们就可以写出Bresenham的伪代码表示：
// k在[0, 1]的Bresenham算法
void Bresenham(int x1, int y1, int x2, int y2) {
float d = 0;
float k = (y2 - y1) / (x2 - x1);
while (x1 != x2) {
plot(x1, y1); // 绘制点
x1 += 1; // x1向后移动一个像素点
d += k;
if (d >= 1) d -= 1;
// 计算y的下一个值
if(d >= 0.5) y1 += 1;
}
}将所有的浮点数转换为整数#
Bresenham之所以比中点画线和DDA算法要好，就是因为它的算法内没有任何的浮点数运算。显然我们还需要改进。
第一个改进的点就是令$e = d - 0.5$，这样的话我们只需要判断$e$是否大于等于0，如果是，则y+1，否则y不动：
$$ y = \begin{cases} y + 1, e >= 0 \\ y, e < 0 \end{cases} $$初值为
$$ e_0 = -0.5 $$递推式变成:
$$ e_{i+1} = d_{i+1} - 0.5 = d_i - 0.5 + k = e_i + k = e_i + \frac{y2 - y1}{x2 - x1} = e_i + \frac{\Delta y}{\Delta x} $$e的更新式子:
$$ 如果e >= 0 那么 e = e-1 $$然后这里的$e_0$是-0.5这点不行，并且在迭代式中还有个可能是浮点数的k，所以我们令
$$ e' = 2e\Delta x $$这样就有了新的初值和递推式：
$$ \begin{matrix} e'_0 = 2e_0\Delta x = 2\times -0.5 \times \Delta x = -\Delta x \\ e'_{i+1} = 2e_{i+1}\Delta x = 2(e_i + k)\Delta x = 2e_i\Delta x + 2k\Delta x = e_i + 2\Delta y \end{matrix} $$即
$$ \begin{matrix} e'_0 = -\Delta x \\ e'_{i+1} = e_i + 2 \Delta y \end{matrix} $$$e’$的更新式子:
$$ 如果e' >= 0那么e' = e' - 2\Delta x $$新的y改变规则就出来了：
$$ y = \begin{cases} y + 1, e' >= 0 \\ y , e' < 0 \end{cases} $$这下所有的变量都是整数，没有任何的浮点数计算了。
那么代码表示如下：
// k在[0, 1]的Bresenham算法
void Bresenham(int x1, int y1, int x2, int y2) {
int dx = abs(x1 - x2),
dy = abs(y1 - y2); // 这里由于dx,dy只是用于e中，所以我们可以简单取正
int e = -dx;
while (x1 != x2) {
plot(x1, y1);
x1 += 1;
e += 2* dy;
if (e >= 0) {
e -= 2 * dx;
y++;
}
}
}这样就完成了。
推广到所有象限#
首先，如果$\Delta y > \Delta x$，那么我们需要将式子中的$\Delta x$和$\Delta y$互换。
其次是x和y的步进问题，这里我们这样：
int sx;
if (x1 > x2) sx = 1;
else if (x1 == x2) sx = 0;
else sx = -1y也是同理，这样完整的程序就是：
void Bresenham(int x1, int y1, int x2, int y2) {
int dx = abs(x1 - x2),
dy = abs(y1 - y2),
sx = x1 > x2 ? 1 : x1 == x2 ? 0 : -1,
sy = y1 > y2 ? 1 : y1 == y2 ? 0 : -1
int e;
if (dx >= dy) e = -dx;
else e = -dy;
while (x1 != x2 && y1 != y2) {
plot(x1, y1)
if (dx >= dy) {
x1 += sx;
e += 2 * dy;
if (e >= 0) {
e -= 2 * dx;
y += sy;
}
} else {
y1 += sy;
e += 2 * dx;
if (e >= 0) {
e -= 2 * dy;
x += sx;
}
}
}
}完整的Nim实现在这里