VisualGMQ的博客

OBB包围盒的碰撞检测(SAT算法)

 2867  6 分钟  

碰撞检测的包围盒一般分为三种：

  • AABB包围盒：就是所谓的无矩形包围盒
  • OBB包围盒：就是可旋转矩形包围盒
  • 多边形包围盒

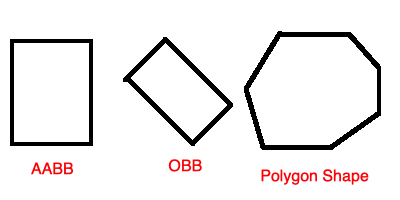
包围盒形状

对于AABB类型的包围盒的碰撞检测很简单，但是对于OBB和多边形的碰撞检测则比较困难。这里主要说明SAT算法，并且将SAT算法应用到OBB包围盒中（多边形同理）。

SAT算法

SAT算法全名为分离轴定律（Separate Axis Theory），它的思想是：

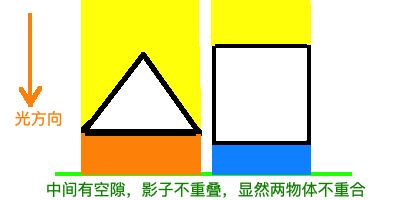
将一束平行光照射到物体上，如果在任何角度的照射下，两个物体的影子都会重合，那么这两个物体一定相交

或者你也可以简单理解为“只要存在一个角度，导致影子不重合的话，就不会相交”或者“只要存在一条直线将两个物体分割开来，那么两个物体必然不相交”。

不相交的情况

那么我们在代码中要怎么实现呢？其实我们不需要“在任意方向上投影”，我们只需要在两个多边形所在的每个边上投影即可：

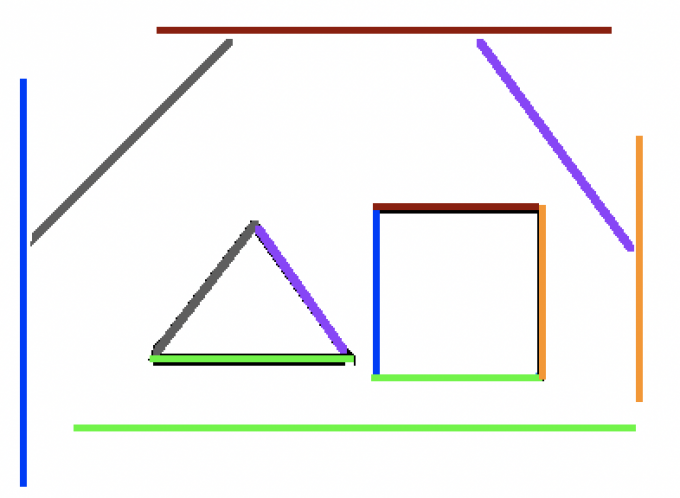
所有的投影轴

如果其中存在任何一个边上的两个物体的投影不重合，那么这两个物体一定是分离的。相反，如果所有投影轴上的投影都是重合的，那么这两个物体一定是重合的。

SAT算法比起其他的碰撞检测算法更加优秀的一点在于：可以在计算的过程中直接得到最小分离向量。所谓最小分离向量就是讲这两个物体分开的长度最小的向量。有了最小分离向量，我们就可以将两个物体分离了。

最小分离向量的大小就是两个物体影子重合长度最小的那个长度（所有影子重合长度的最小值），方向就是重合长度最小的影子所在的投影轴的方向

SAT是一个很通用的算法，普通的AABB或圆的碰撞检测算法也是可以从SAT推导出来的。

实现

我们这里只实现OBB和OBB的碰撞检测，多边形的道理是一样的。

思路

遵循大问题分解成小问题原则，首先考虑：如果对两个OBB使用SAT，由于OBB的对边是平行的，所以实际上不需要四条投影轴，而是两条就行了，这两条分别是：Vec2(obb1.rotation.GetAxisX(), obb1.rotation.GetAxisY()),Vec2(obb2.rotation.GetAxisX(), obb2.rotation.GetAxisY()) 。

接下来要考虑在这两条投影轴上如何进行投影。这里我的方法是：将其中一个OBB的中点变为原点，并且将其xy轴视为新的xy轴，然后将两一个OBB在这个新坐标系下进行投影：

SAT思路

这样的话，我们就连第一个OBB的投影都不需要算了：其在x轴上的投影区间就是[obb1.-half_w, obb1.half_w]，在y轴上的投影区间就是[obb1.-half_h, obb1.half_h]。这样我们只需要将注意力放到另一个OBB的投影上即可。

这样的话，剩下的问题就变为：给定一个坐标系，计算OBB中一个边在这个坐标系下的投影。我们只需要分别对这个OBB的四个边进行计算，就可以得到其所有边的投影区间了。

一些数据结构

首先，为了表示几何体和投影长度，我们要准备一些数据结构：

OBB

OBB的表示如下：

1
2
3
4
5
6
7

struct OBB{
	Vec2 center;
	Rot rotation;
	real half_w;	//宽度的一半
	real half_h;	//高度的一半
	OBB(Vec2 cent, real degree, real w_2, real h_2)；
};

其中Vec2是2D向量的类，由于向量计算的表示基本都差不多，在此不列举Vec2类的声明。

Rot是使用正弦值和余弦值表示旋转的类（借鉴自Box2D），之所以使用正弦值和余弦值表示，是为了方便得到局部坐标轴：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

#include <cfloat>
#define FLT_EQ(x, y) (abs(x-y)<=FLT_EPSILON)

class Rot{
public:
	Rot():s(0),c(0){}
	Rot(real degree){
    Set(degree);
  }
  void Set(real degree){
    s = sin(DEG2RAD(degree));
    c = cos(DEG2RAD(degree));
  }
	real GetDegree() const{
    return asin(s);
  }
  //通过这个函数得到OBB旋转后的X轴
	Vec2 GetAxisX() const{
    return Vec2(c, s);
  }
  //通过这个函数得到OBB旋转后的Y轴
	Vec2 GetAxisY() const{
    return Vec2(-s, c);
  }
	bool operator==(const Rot& rot) const{
    return FLT_EQ(rot.s, s)&&FLT_EQ(rot.c, c);
  }
	bool operator!=(const Rot& rot) const{
    return !(*this==rot);
  }
private:
	real s;	//sin value
	real c;	//cos value
};

FLT_EQ宏是使用减法来判断两个浮点数是否相等的宏，FLT_EPSILON则是C++头文件<cfloat>中的常量。

区间

由于我们要计算投影的重合长度，所以这里先定义区间：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

class Range{
public:
	Range(real a, real b); //自动判断谁大谁小，并赋值给min和max
	real Min() const;	//返回min
	real Max() const;	//返回max
	real Len() const; //返回max-min
private:
	real min;
	real max;
};

函数

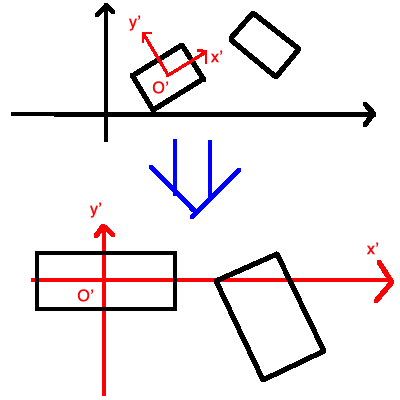
首先来看一下如何将一个OBB的所有点转换到另一个坐标系，如果你学过线性变换会很简单，但是我们这里仍然使用向量数学来推导一下，看图即可明白:

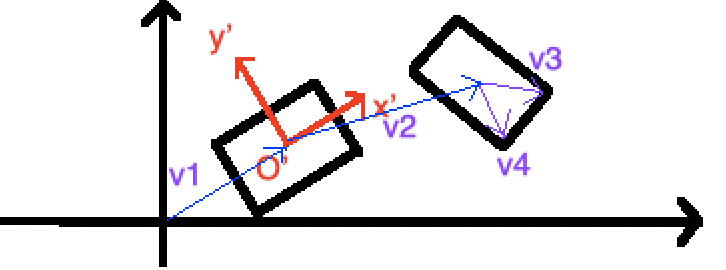
OBB的坐标变换

这里v1显然是obb1.center，v2则可以通过obb2.center-obb1.center得到。

然后是v3和v4，有了v3和v4我们才能得到OBB的四个点。由于我们可以通过obb2.rotation.GetAxisX(), obb2.rotation.GetAxisY()来得到其x，y轴的单位向量，所以: $$ axis_x = obb2.rotation.GetAxisX();axis_y=obb2.rotation.GetAxisY() $$

$$ v3 = (obb2.center+axis_xobb2.half_w,obb2.center+axis_yobb2.half_h) $$

$$ v4 = (obb2.center+axis_xobb2.half_w,obb2.center-axis_yobb2.half_h) $$

那么显然，其四个点相对于O'的坐标就是： $$ dir = obb2.center-obb1.center;p1=dir+v3-v4;p2=dir+v3+v4;p3=dir-v3-v4;p4=dir-v3+v4 $$ 接下来就需要将其四个点的坐标转化为在x'O'y'下的坐标了。很简单，将p1,p2,p3,p4投影到x'和y'上，计算出新的坐标即可。

那么最后转换的代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

Vec2 axis_x = obb2.rotation.GetAxisX()*obb2.half_w;	
Vec2 axis_y = obb2.rotation.GetAxisY()*obb2.half_h;
Vec2 points[4] = {
  axis_x+axis_y + obb2.center,
  axis_x-axis_y + obb2.center,
  -axis_x-axis_y + obb2.center,
  -axis_x+axis_y + obb2.center
};
Coord coord(obb1.center, obb1.rotation);
for(int i=0;i<4;i++)
  points[i] = CoordConvert(points[i], coord);

这里Coord是用于表示坐标系的结构体，CoordConvert是将点转化到坐标系的函数:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

struct Coord{
	Rot rotation;
	Vec2 center;
	Coord(Vec2 cent, real degree);
	Coord(Vec2 cent, Rot rot);
};

Vec2 CoordConvert(Vec2 point, Coord coord){
	Vec2 dir = point-coord.center;
  //Dot是两个向量的点积
	return Vec2(Dot(dir, coord.rotation.GetAxisX()), Dot(dir, coord.rotation.GetAxisY()));
}

然后就要考虑，如果将已经转化过的坐标投影到新坐标系下了：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

//assume points[4] are relate coord
bool __linevsobb(Vec2 axis, real half_len, Vec2 points[4]){
	bool result = false;
	for(int i=0;i<3;i++)//这里分别对OBB2的四条边进行投影和判断
		result = result||__lineprojline(axis, half_len, points[i], points[i+1]);
	result = result||__lineprojline(axis, half_len, points[3], points[0]);
	//使用逻辑或表示如果存在两条边的投影重合，则相交
	return result;
}

//assume p1, p2 is local coord
//这个函数会将边投影，并且计算出投影的重合度
bool __lineprojline(Vec2 axis, real half_len, Vec2 p1, Vec2 p2){
	Range r1(ProjectEffect(p1, axis), ProjectEffect(p2, axis)),	//将p1,p2投影到坐标系
		r2(-half_len, half_len);	//由于OBB1原本就是以自己为坐标系，所以我们就直接给出其投影区间，不用计算
  //计算重合度
	if(__get_range_cover_len(r1, r2)==0)	//如果重合长度为0，那么返回false，表示这两条边没有重合
		return false;
	return true;
}

//计算两个区间重合长度的函数
real __get_range_cover_len(Range range1, Range range2){
	if(range1.Min()<range2.Min()){
		if(range1.Max()>range2.Min() && range1.Max()<range2.Max())
			return range1.Max()-range2.Min();
		else if(range1.Max()>=range2.Max())
			return range2.Len();
	}else{
		if(range1.Min()<range2.Max())
			if(range1.Max()<=range2.Max())
				return range1.Len();
			else if(range1.Max()>range2.Max())
				return range2.Max()-range1.Min();	
	}
	return 0;
}

这样最后我们将上面的函数整合起来：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

bool __onewayobbtest(const OBB& obb1, const OBB& obb2){
  //先进行坐标变换
	Vec2 axis_x = obb2.rotation.GetAxisX()*obb2.half_w;	
	Vec2 axis_y = obb2.rotation.GetAxisY()*obb2.half_h;
	Vec2 points[4] = {
		axis_x+axis_y + obb2.center,
		axis_x-axis_y + obb2.center,
		-axis_x-axis_y + obb2.center,
		-axis_x+axis_y + obb2.center
	};
	Coord coord(obb1.center, obb1.rotation);
	for(int i=0;i<4;i++)
		points[i] = CoordConvert(points[i], coord);
  //然后判断在(0,1)轴上投影是否重合
	if(!__linevsobb(Vec2(0, 1), obb1.half_h, points))
		return false;
  //判断在(1,0)轴上投影是否重合
	if(!__linevsobb(Vec2(1, 0), obb1.half_w, points))
		return false;
	return true;
}

注意这个函数只是将一个OBB的四个边作为投影轴。SAT要求另个多边形的所有边都得作为投影轴，所以最后：

1
2
3
4

bool OBBvsOBB(const OBB& obb1, const OBB& obb2){
  //如果所有投影轴中存在重合，返回true表示碰撞了
	return __onewayobbtest(obb1, obb2) && __onewayobbtest(obb2, obb1);
}

结果：

结果

SAT的优缺点

优点：

  • 可以对于任意的多边形进行碰撞检测，甚至是圆和多边形的碰撞检测（见参考中的网页）
  • 可以得知最小分离向量

缺点：

  • 计算量很大

对OBB的SAT优化

有一个优化方式是，如果两个OBB的旋转角度一样的话，可以直接通过坐标变换将这个问题转化为两个AABB的碰撞检测问题：

1
2
3
4
5
6
7

bool OBBvsOBBSame(const OBB& obb1, const OBB& obb2){
	Coord coord(obb1.center, obb1.rotation);
	Vec2 relate_center = CoordConvert(obb2.center, coord);
	AABB aabb1(-obb1.half_w, -obb1.half_h, obb1.half_w, obb1.half_h),
		aabb2(relate_center.x-obb2.half_w, relate_center.y-obb2.half_h, relate_center.x+obb2.half_w, relate_center.y+obb2.half_h);
	return AABBvsAABB(aabb1, aabb2);
}

这样可以避免投影，节省很多的速度。

参考

CSDN博客

N网站的教程

gamedevelopment网站的教程，很全

updatedupdated2023-06-182023-06-18